Twitter'da Paylaş Facebook'ta Paylaş 'te Paylaş s4 (30° – 60° – 90°) Üçgeni ;(A açısı = 90 (B açısı = 75 (C açısı = 15 açıları ise uzunlukları şu kural doğrultusunda

Ozel Ucgenler Nelerdir Eodev
15 75 90 üçgeni ve özellikleri
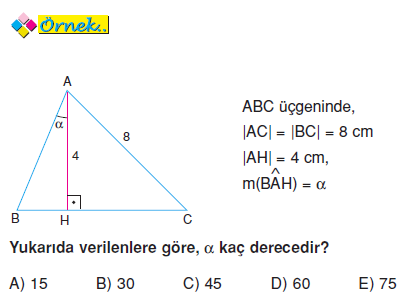
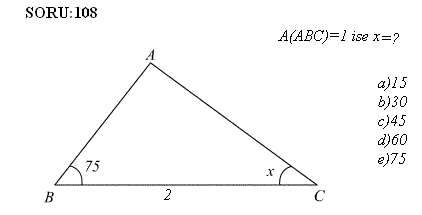
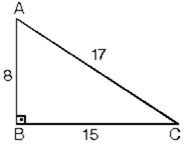
15 75 90 üçgeni ve özellikleri-15° – 75° – 90° Dik Üçgeni Yukarıda verilenlere göre, AC kaç cm dir?A)8 B)6 C)5 D)4 E)3 30° – 30° – 1° Üçgeni 1° nin karşısındaki kenar, 30° nin karşısındaki kenarın katıdır Yukarıda verilenlere göre, x kaç cm dir?



Dik Ve Ozel Ucgenler 1
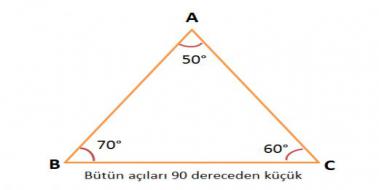
Dar Açılı Üçgen Özellikleri Dar açılı üçgenlerin hiç bir iç açısı 90 derece olamaz Eğer doksan derece varsa bu dik açılı bir üçgendir Diğer iç açılarının 90 dereceden küçük olması üçgenin dar açılı olduğunu göstermez Örneğin açıları 30,60,90 olan bir üçgen dar açılı değil dik açılıdır5 (30° 30° 1°) Üçgeni;üçgeni şükela tüm ü bugün uzun veya en kısa köşegeni verilip sekizgenin alanı istenildiğinde yararlanılır bi de bunun kankası var (bkz üçgeni) 03 jack nicholson (bkz hayırlı olsun kardeş dershaneye yazılmışsın) 04 hele bi yarin olsun da o zaman dusunuruz üçgenine tamamlanarak formülü
Son olarak 3 4 5 üçgeninin trigonometrik bağıntılarını da paylaşalım Sin37 = 3 / 5 = 0,6 Sin53 = 4 / 5 = 0,8 Cos37 = 4 / 5 = 0,8 Sin53 = 3 / 5 = 0,6 Tan37 = 3 / 4 = 0, 75 Tan53 = 4 / 3 3 4 5 üçgeni soruları sadece geometride değil aynı zamanda fizikte de karşımıza çıkmaktadır Bu nedenle bu üçgenin açı veBu ders notumuzda Geometri dersinin Özel Üçgenler başlığı altında; Etiketle r 15 75 90 üçgeni özelliklerinin ispatı, 15 75 90 üçgeni özellikleri nelerdir, 15 75 90 üçgeni özellikleri nerden geliyor, hipotenüs neden yüksekliğin dört kat ı s # Bora Arslantürk # ispat # matematik # son # video Tweet Share Pin it zaman Bunu Epostayla Gönder BlogThis!
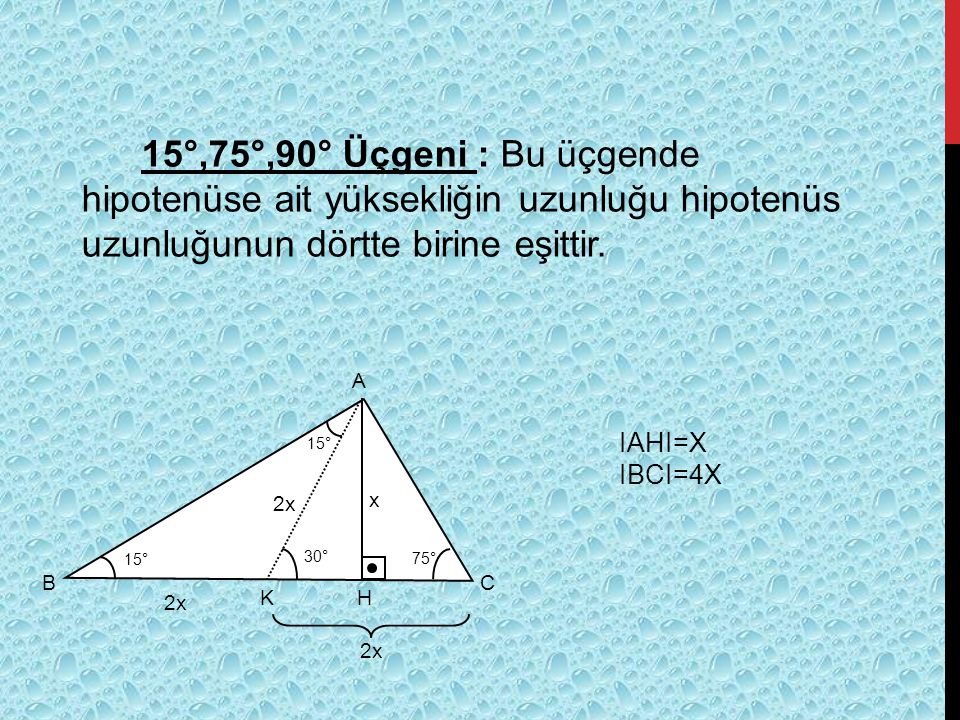
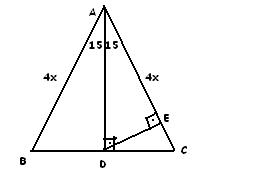
Dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir (a2=b2c2) – Pisagor bağlantısı ← Dünyamızın içABE üçgeni (15 75 90 ) üçgenidir ABE üçgeninde E nin AB ye en yakın uzaklığı hipotenüse ait yükseklik; 1575 90 Üçgeni Bu üçgende hipotenüsün yüksekliğine x dediğimiz zaman hipotenüsün uzunluğu bu ölçünün 4 katı yanı 4x olmaktadır İkizkenar Üçgen Özellikleri



Ozel Ucgenler Konu Anlatimi



Dik Ucgen Konu Anlatimi Bilgicik Com Bilgicik Com
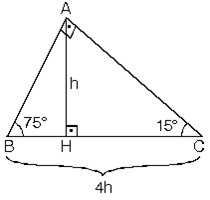
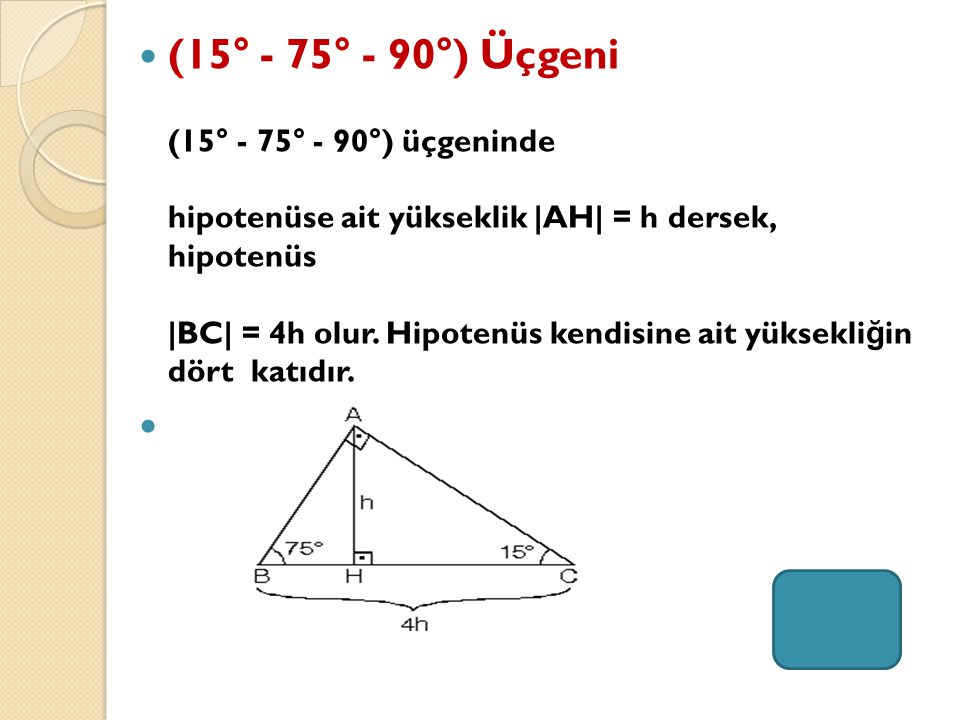
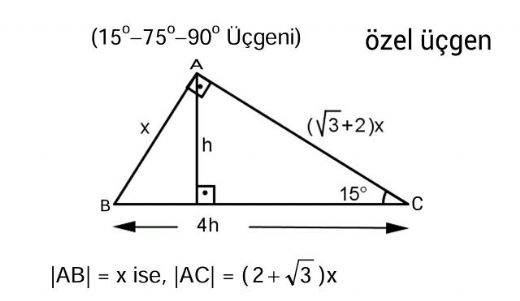
15 75 90 Üçgeni Özellikleri Sorularda bir üçgene, bir dikdörtgene ya da herhangi bir çokgene dikme indirerek veya bir çizgi çekerek karşınıza 15 75 90 üçgeninin çıkmasını sağlayabilirsiniz Bu üçgeni bulduktan sonra aşağıdaki kuralları aklınızdan çıkarmamanız gerekir Dik üçgendir Bu üçgenin iki dar açısını topladığınızda dik açısını bulursunuzHipotenüs üçgenin en uzun kenarıdır;(15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, Hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır İKİZKENAR ÜÇGEN İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem açıortay, hem de kenarortaydır 1 Bir üçgende, açıortay aynı zamanda yükseklik ise bu üçgen




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri




Ozel Ucgenler Nelerdir Eodev
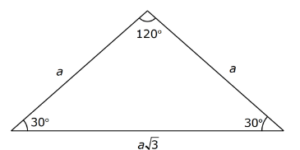
Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 1933 üçgeni mrdanqerous bu konuyu Özel geometri soruları forumunda açtı Cevap 2 Son mesaj 18 Kas 12, 1806 ABC üçgeni Enes Ergel bu konuyu 9 sınıf matematik soruları forumunda açtı Cevap 2 Son mesaj 125 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğer




Ucgende Acilar




Rox Wood Aluminyum Ucgen Marangoz Gonye 175 Mm Fiyati
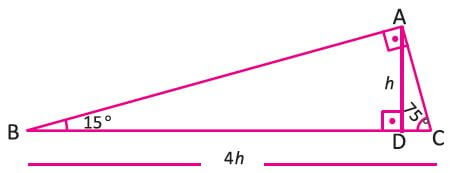
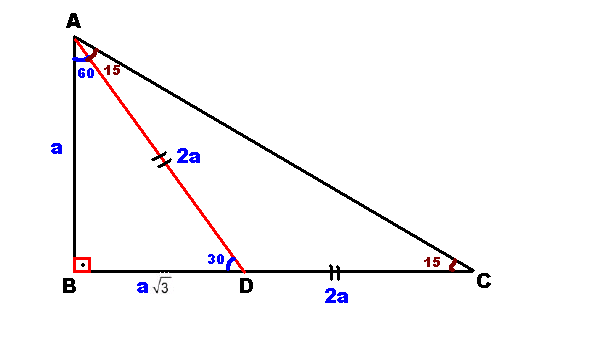
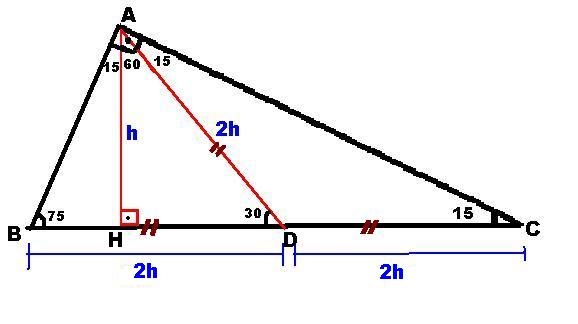
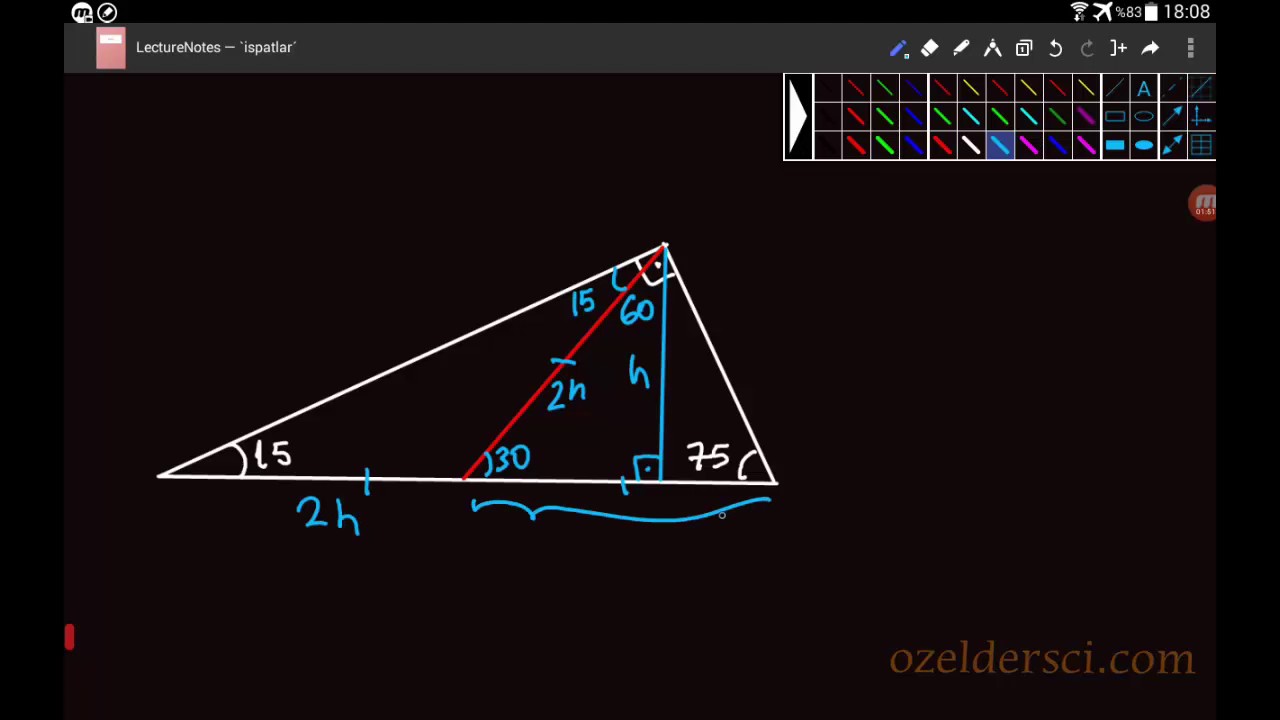
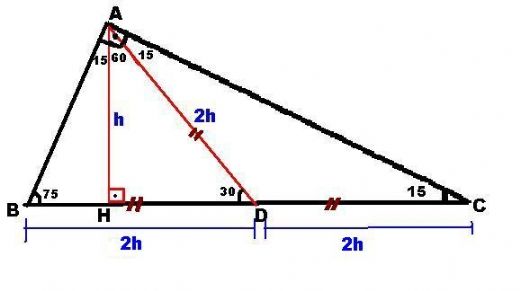
7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = Üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün 1/4 Üçgeni (h4h) İSPAT üçgeninde hipotenüse indirilen yüksekliğe h diyelim Daha Sonra Süper üçlüyü kullanmak için hipotenüsü iki eşit parçaya bölecek kenarortayı çizelim 3 adet üçgenimiz oluştu () () (0) 30⁰'nin karşısına h dediğimiz zaman 90⁰'nin karşısına 2h




15 75 90 Ucgeninin Ispati




Kisa Yollar 2 15 75 22 5 67 5 Derecenin Trigonometrik Degerleri Youtube
5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur 15 75 90 üçgeninde 15 derecelik açının karşısında ki kenar 1cm olarak düşünülür ise 75 derecelik açının karşısında ki kenar 2kök 3 olmaktadır Ayrıca hipotenüse indirilen dikme 1 cm iken indirilen kenar 4 cm olmaktadır Alanı da indirilen dikme uzunluğu ile kenar uzunluğunun yarısı alınarak hesaplanır Son Güncelleme 15 75 90 Üçgeni ileDİK ÜÇGENİN ALANI Diküçgenin alanı, dik kenarların çarpımının yarısıdır WordPresscom'da bir web sitesi veya blog




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu



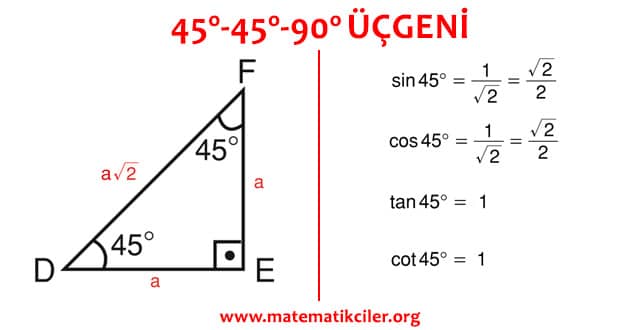
45 45 90 Ucgeni Matematikce
Üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün katıdır EN İYİ CEVABI Safi verdi 22,5 67,5 90 üçgeninin ve üçgeninin özelliklerini Açılarından ötürü özel dik üçgenlerdir ve özellikleri şöyledir Sponsorlu Bağlantılar 1 22,567,590 Üçgeni Bu üçgende ise 22,5°'lik açının karşısındaki dik kenar 1 cm ise, 67,5 cm'lik kenarın karşısındaki kenar cm olur6 (15° 75° 90°) Üçgeni ;




Nature And Genesis Of Potassic High Basr Granitoids Associated With Syn Convergent Extension In Nw Turkey Sciencedirect



Dik Ucgende Trigonometri Bikifi
Dik Üçgen, Pisagor Bağıntısı, Özel Dik Üçgenler, İkizkenar dik üçgen, (30° – 60° – 90°) Üçgeni, (30° – 30° – 1°) Üçgeni, (15° – 75° – 90°) Üçgeni, Öklit Bağıntıları, İkizkenar Üçgen, Eşkenar Üçgen vb içerikler hakkında detaylı bilgileri bulabilirsiniz 15 75 90 Üçgeni Özellikleri ve Kuralı Cevap bırakın Yanıt İptal Et Eposta hesabınız yayımlanmayacak Cevap verdiğiniz için teşekkürler, sitemizdeki diğer içerikleri okumanızı öneriyouz Ad ve e posta bilgilerimi kaydet oturum aç Son Eklenenler Kapıda Ödeme Olan Siteler 21 Güncel Haz 23, 21 Ses Kaydını Videoya Çevirme Haz 22, 21 Twitch Video İndirme(15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC




15 75 90 Ucgeni Webders Net



Ozel Ucgenler Ppt Video Online Indir
2 (5 12 13) Üçgeni;(15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz ) Tüm Öğrencilerimize İyi Dersler Diliyoruz ) Seyfettin KAHVECİ (15 75 90) Üçgeni ;DİK ÜÇGEN 16 15 75 90 ÜÇGENİ kaydeden Mustafa YAZAGAN 62 Kişisel Gelişim Geometri Psikoloji Science Harfler Eğitim Banyo Daha fazla bilgi Bunun gibi daha fazlası Gizlilik



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir



Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com
15 75 90 üçgen özelliği ve 15 75 90 üçgeninin 2 pratik kuralı ve örnek çözümlü sorularPratik Geometri Yöntemleri videolarımda sizlere mantık ve pratik yönte1 (3 4 5) Üçgeni;üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar 2 3 {\displaystyle 2 {\sqrt {3}}} cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu




Pdf Influence Of Foreign Ions On The Crystal Structure Of Batio3



15 75 90 Ucgeni
15 – 75 – 90 DİK ÜÇGENİ Eğer bir 15 75 90 üçgeni düşünecek olursak;(15 75 90) Üçgeni (45 45 90) Üçgeni;Quote Orijinalden alıntı brknzbz üçgeninde şu bağıntılar vardır 1 (kök31)k (kök31)k (2kök2)k sırasıyla derecelerin karşılarındaki kenarların aralarındaki bağıntıdır bu 2 15 derecenin hemen yanına doğru bir doğru parçası indirerek ikizkenar üçgen oluşturup (1515 derece şeklinde) küçük bir 0 ve üçgeni oluşturmak




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
3 İkizkenar dik üçgen;5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 15 ve 60 olarak böldüğünüzde ise karşınıza bir 30 60 90 üçgeni ve de diğer tarafta kalan açıları 15 15 150 olan bir ikizkenar üçgen çıkacaktır bu durumda şöyle bir sonuç çıkar karşımıza 15 derecenin karşısındaki kenara a değerini verirsek, 75 derecenin karşısındaki kenar da 2aakök3 olacaktır 90'nın karşını da pisagor teoreminden hesaplayın, işiniz




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Geometri Formulleri Sezgin Oner Matematik Yayinlari Facebook
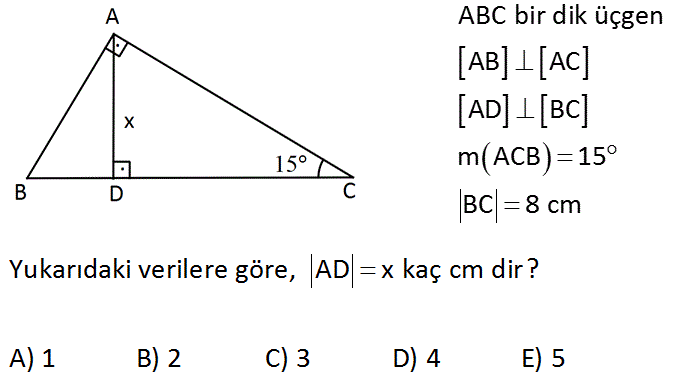
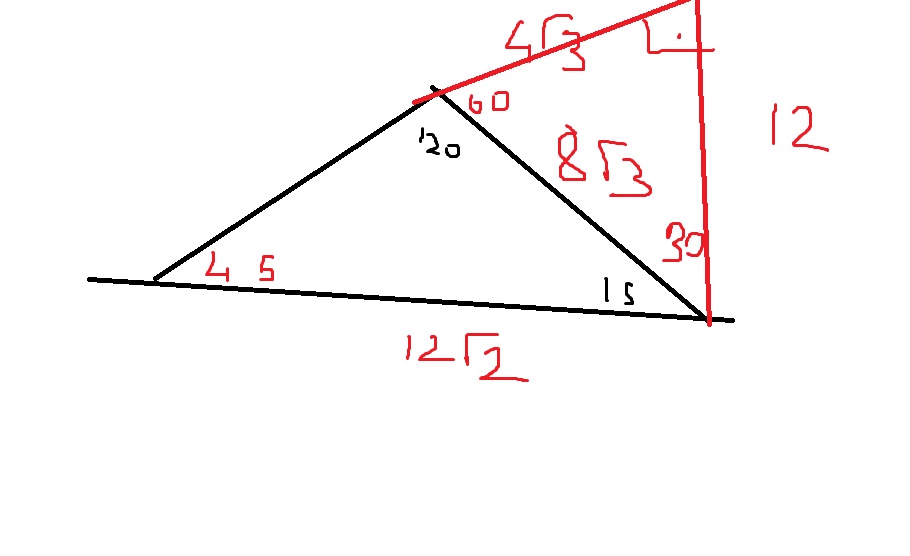
özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır 5 ayrıca 75 ten uzatılacak kol ile 15 15 eş üçgeni ve 30 60 90 dik üçgeniA) 2 3 4 B) 2 3 6 C) 4 3 2 D) 4 3 4 E) 4 3 6 wwwmatematikkolaynet Çözüm 15 75 90 üçgeninden AD 8 4 3 olur ABD ve HAD üçgenleri benzer üçgenlerdir 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 in karşısındaki kenar "2aakök3" aynı yolla 22



15 75 90 Ucgeni




30 60 90 Ucgeni Ve Ozellikleri Not Bu
15 75 90 Üçgeni Özellikleri 15 75 90 Üçgeninde Kenarların Oranı 15 75 90 üçgeninde kenarlar arasında belirli bir oran bulunması zorunluluğu vardır Bu oran formül ezberlendiği zaman rahat bir şekilde ortaya çıkartılabilir Eğer formülü ezberlemezseniz farklı yöntemlerle bu hesaplamaları yapabilirsiniz Fakat oldukça yoğun bir zaman ayırmanız gerekiyorTeoremin kendine has özelliklerinin olmasıdır Bu özellikler başka hiç bir teoremde yada cisimde bulunmamasıdır En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmasıdır Üçgenlerin 3 adet kenarı ve 3 adet açısı vardır 15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğer açının ölçüsünü vermektedir İki dar açının birbirine oranı 1/5 olmalıdır Hipotenüse ait yükseklik hipotenüs uzunluğunun 4'te 1'idir



ベスト 75 15 90 Ucgeni Ozellikleri シモネタ



15 75 90 Ucgeni Ozellikleri Acilar Gen Tr
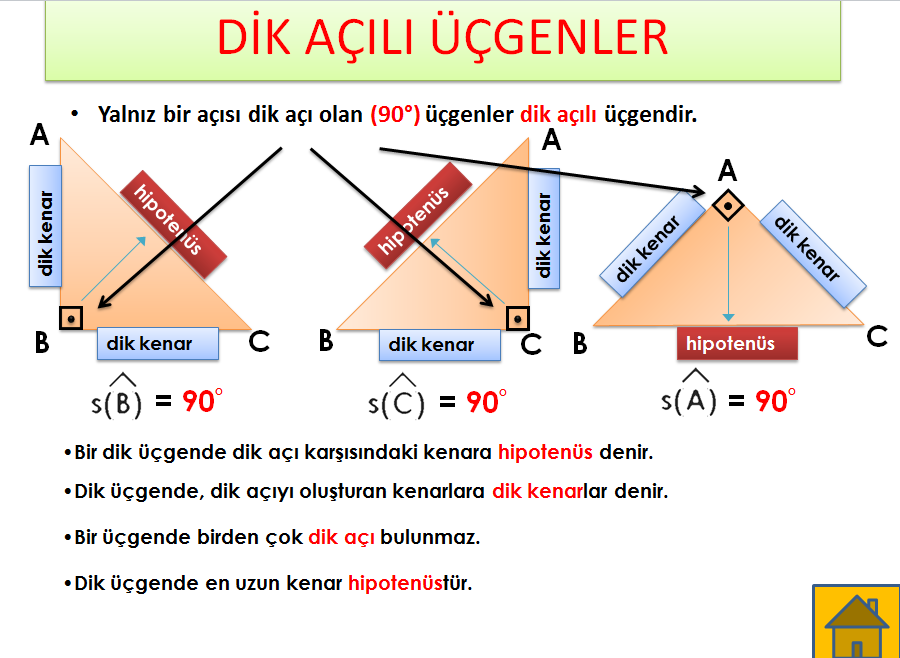
Hayyam Üçgeni Özellikleri (Posteri) en uygun fiyat ve hızlı kargo avantajıyla sahip olabilirsiniz Hayyam Üçgeni Özellikleri (Posteri) yorum ve fiyatını inceleyin Sipariş ve Destek 0850 840 78 16 0346 241 42 42 Bulunan Ürünler Tüm Sonuçlar İçin Tıklayınız Kayıt Ol;Dik açılı üçgenlerin özellikleri Bir açısının ölçüsü 90°'ir 90°'nin karşısındaki kenar hipotenüstür ve diğer kenarlar dik kenarlardır;15 75 90 Üçgeni Özellikleri ve Kuralları Geometri dersi için özel üçgenlerin büyük önemi bulunmaktadır Özellikle bu tür üçgenlerin özellikleri bilindiğinde pek çok soru çok rahat bir şekilde çözülmektedir 15 75 90 üçgeni de bu özel üçgenler arasında özellikle bilinmesi gereken üçgenler arasında yer almaktadır




Ucgen Ve Ozellikleri Pisagor Arican Fen Bilimleri Facebook




15 75 90 Ucgeni Ozelliklerinin Ispati Ozeldersci
12 A B C E 75 15 H 15 x EH = x uzunluğudur Buradan AB = 4 EH olduğundan, 12 = 4 x x = 3 br bulunur Cevap A'dır (vii)(30 30 1 ) ÜÇGENİ A B C 30 30 1 x x x 3 Bu üçgende, 1 nin karşısındaki kenar, eş kenarlardan birinin 3 katına eşittir AB = AC m Geometrideki özel üçgenlerden biri de 15 75 90 üçgeni dediğimiz özel üçgendir Bu üçgen karşımıza diğer özel üçgenler kadar yaygın çıkmasa da üçgenini bilmek bize geometride birçok yerde fayda sağlayacaktır Çünkü bu üçgen türü karşımıza tek başına çıkmasa dahi soru içerisinde çıkabilmektedir 15 75 90 üçgeni ile ilgili özellikleri15 75 90 ÜÇGENİ VE ÖZELLİKLERİ ÖKLİT BAĞINTILARI HAKKIMIZDA Bu sayfada yer alan bilgilerin her hakkı, aksi ayrıca belirtilmediği sürece TestDefteriCom'a aittir Sitemizde yer alan dosya ve içeriklerin telif hakları dosya ve içerik gönderenlerin kendilerine veya yetki verdikleri kişilere aittir Sitemiz hiç bir şekilde kâr amacı gütmemektedir ve sitemizde yer alan



Acill Ozel Geometri Sorusu
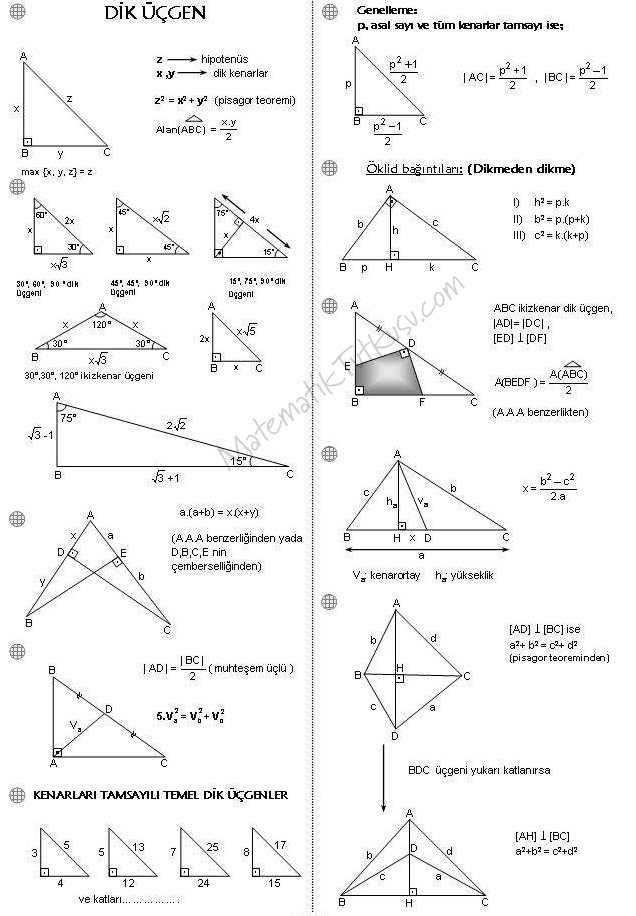



Ozel Ucgenler Formulleri
1 Bir Üçgenin iç açılarının toplamı 180° dış açılarının toplamı 360°'dir 2 Üçgende bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir 3 Bir dik üçgenin dik kenarlarına 'a' ve 'b' dersek hipotenüs'ün karesi bu kenarların uzunluklarının karelerinin toplamınaİkizkenar Üçgenler İkizkenar Üçgenler konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz ) Tüm Öğrencilerimize İyi Dersler Diliyoruz ) Seyfettin KAHVECİ0 Sepetim Tüm Kategoriler




15 75 90 Ucgeni Akilli Geometri




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube
15° 75° 90° üçgeni, Özel bir üçgendir Matematikte özel kavramı;Sponsorlu Bağlantılar Dik açılı üçgen, iç açılarından biri 90° olan üçgendir Çemberde çapı 7 24 25 ÜÇGENİ ÖZELLİKLERİ Dik üçgenlerde dik kenarların uzunluklarının karelerinin toplamı hipotenüsün karesini vermektedir Bu bağlantıya uyan bazı tam sayılı özel dik üçgenler bulunmaktadır Bu özel üçgenlerden bir tanesi ise 7 24 25 üçgenidir Bu özel üçgenin kenar uzunlukları 7 24 25 ile orantılı olarak artıp azalmaktadır Elimizdeki bu üçgen 7 metre




Late Jurassic Magmatism And Stratigraphy In The Eastern Sakarya Zone Turkey Evidence For The Slab Breakoff Of Paleotethyan Oceanic Lithosphere The Journal Of Geology Vol 125 No 1




Dik Ve Ozel Ucgenler
15 75 90 üçgeni özelliklerinin ispatıDaha fazla ispat için http//wwwozelderscicom/matematikformullerininteoremlerininhtmlSitemizi ziyaret eAD C üçgeni 15 75 90 üçgenidir 15 75 90 üçgeninde hipotenüse inen yükseklik, hipotenüsün 4' te 1'i dir 4 2 x 2 cm bulunur 4 12 ABC eşkenar üçgen, AB // AD AE AD ED 2 cm Yukarıdaki verilere göre, BE x kaç cm dir? 15 75 90 Üçgeni (15°, 75°, 90°) dik üçgeninde hipotenüsü ait yükseklik hipotenüsün dörtte birine eşittir 30 30 1 Üçgeni 30 – 30 – 1 ikizkenar üçgeni iki adet 30 – 60 – 90 dik üçgeninden oluşur 1 0 'nin karşısındaki kenar ikiz kenarların √3 katına eşittir Dik Üçgen ve Öklid Kuralları Dik üçgenlerde 90°'lik açının bulunduğu köşeden




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Ozellikleri Ve Sorulari
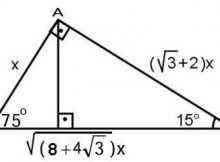



最高75 15 90 Ucgeni Kurali 最高のぬりえ
15 75 90 üçgeni özellikleri Bir dik üçgendir İki dar açısının toplamı dik açısını vermektedir İki dar açı karşısındaki dar kenarlarının toplamı her daim dik açının karşısındaki geniş kenar uzunluğunu vermek zorundadır İki dar açının oranı 1/5 üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik




Dik Ve Ozel Ucgenler 1




Origin And Metamorphism Of Corundum Rich Metabauxites At Mt Ismail In The Southern Menderes Massif Sw Turkey Aydogan 12 Resource Geology Wiley Online Library




Net Fikir Dik Ucgen Ve Temel Ozellikleri




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
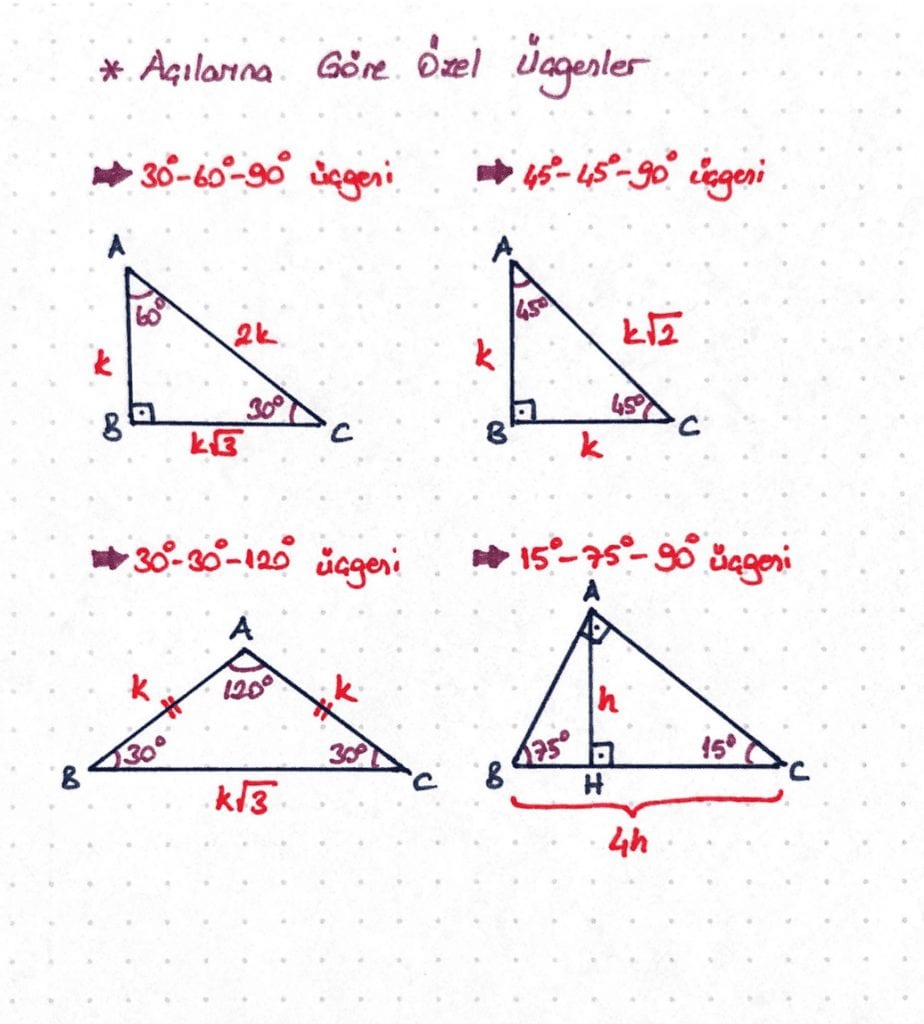



15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Evde Egitim Matematik Felsefesi




Dortgen Vikipedi Cute766




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger




Matematik Ogrenebilir Ppt Indir




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
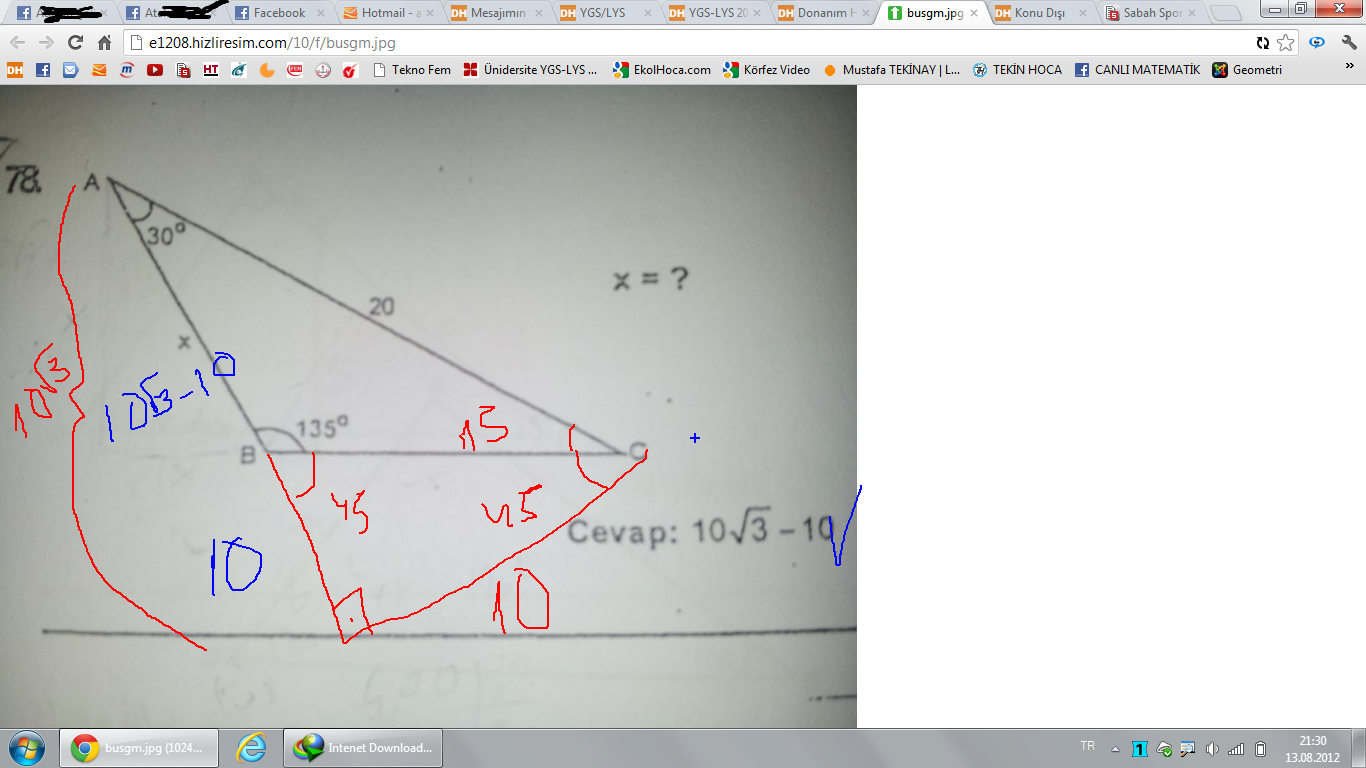



15 75 90 Ucgeni




135 30 15 Ucgenini Aciklayabilir Misiniz Eodev Com




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




15 75 90 Ucgeni Not Bu
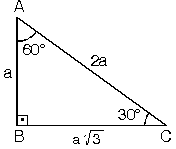



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



15 75 90 Ucgeni 2 3 Ispat



75 Li Bir Ucgen




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube



Geochronology Petrogenesis And Tectonic Importance Of Eocene I Type Magmatism In The Eastern Pontides Ne Turkey Springerlink




15 75 90 Ucgeni Pow Bylge



45 45 90 Ucgeni Matematikce




15 45 1 Ozel Ucgeni Var Mi Varsa Kurali Nedir Eodev Com




Ucgenler Ozel Ozel Ucgenler Ucgen Cesitleri Ucgenlerin Ozellikleri Pisagor Bagintisi Ile Ilgili Konu Anlatimlar Matematik Dersi Ile Ilgili Konu Anlatimlar Ornekler Cozumlu Sorular
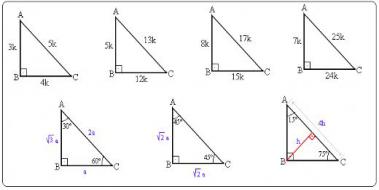



Dik Ucgen Ozellikleri Nelerdir Ucgen Gen Tr




Acilar Ve Ucgenler
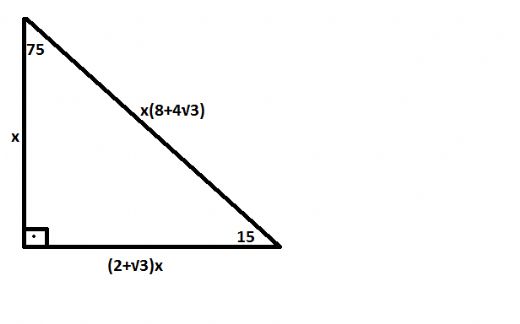



15 75 90 Ucgeninin Ozellikleri Nelerdir Ucgen Gen Tr
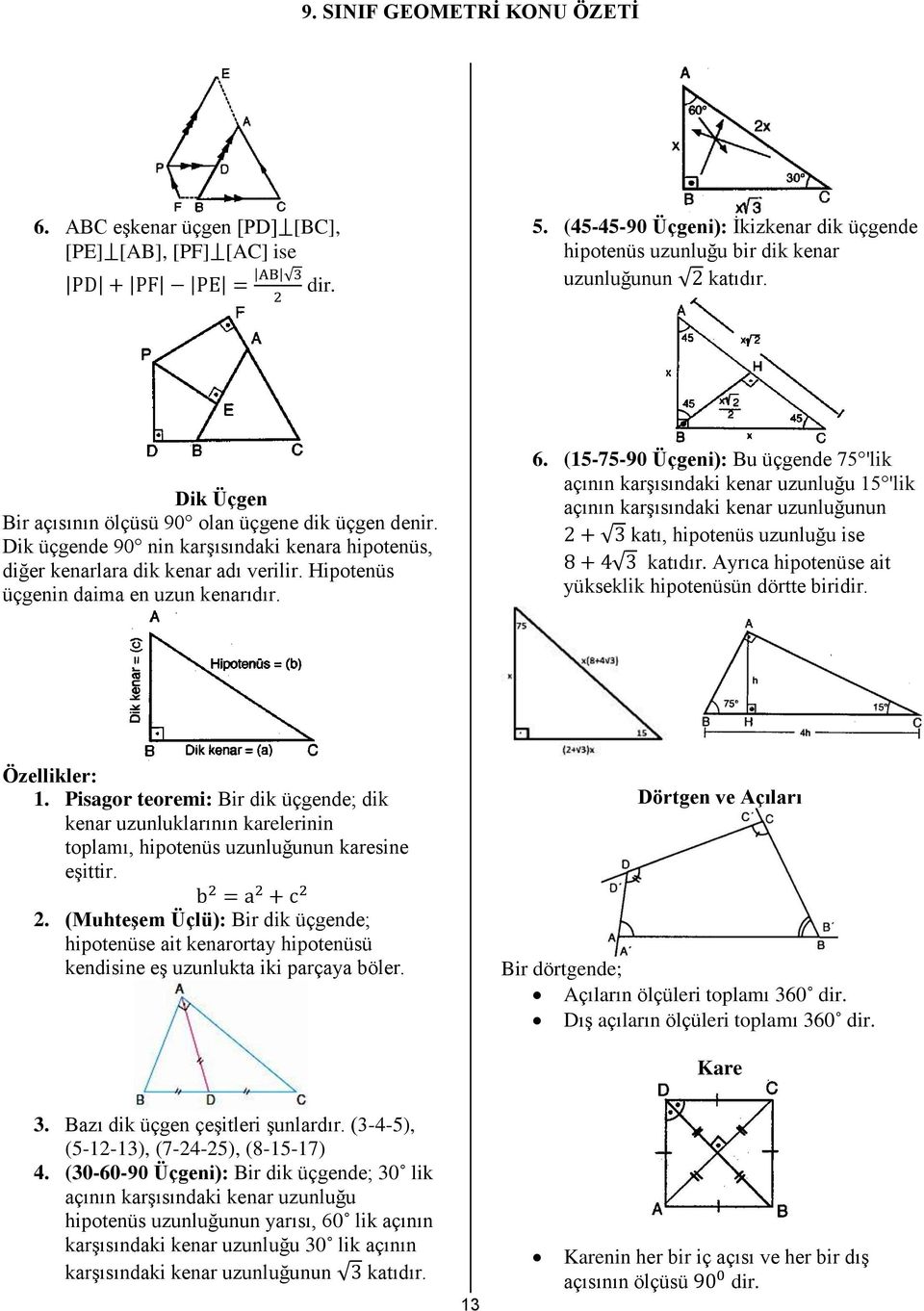



9 Sinif Geometri Konu Ozeti Pdf Ucretsiz Indirin




2 Kok 5 3 Ucgeni
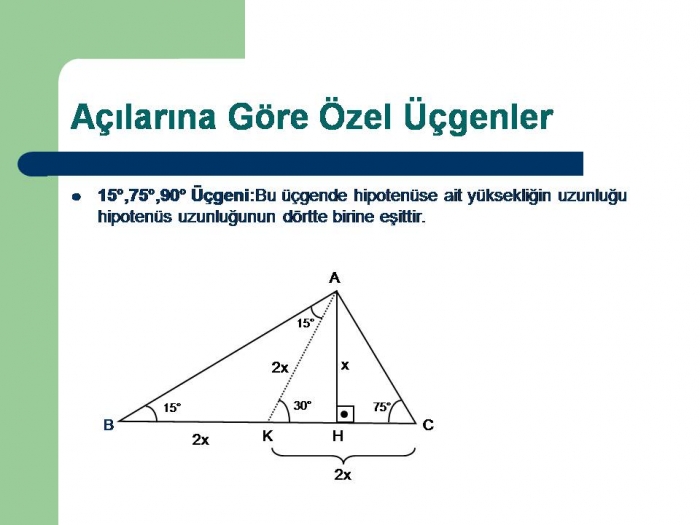



15 75 90 Ucgeni Uludag Sozluk




Geochemistry Of The Middle Jurassic Sediments In Gumushane North Eastern Turkey Implications For Weathering And Provenance Saydam Eker Geological Journal Wiley Online Library




Dershane Osym Lys Ygs Video Ders Konu Anlatim Izle On The App Store



15 75 90 Ucgeni Kenar Bagintisi Ispat



15 75 90 Ucgeni H 4h Ispat



90 75 15 Ucgeni 90 75 15 Ucgeni Ozellikleri Ucgen Gen Tr



1



Dik Ve Ozel Ucgenler 1




15 75 90 Ucgeninin Ozelligi Nedir Eodev Com




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
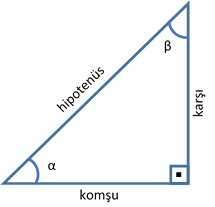



Dik Ucgende Trigonometrik Hesaplamalar




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List




45 45 90 Ucgen Ozellikleri



2



1




15 75 90 Ucgeni Ozellikleri Ve Kurallari




Pdf Influence Of Foreign Ions On The Crystal Structure Of Batio3



1




Dik Acili Ucgenlerin Ozellikleri Nelerdir Dik Ucgenlerin Temel Ozellikleri




3 4 5 Ucgeni Ve Ozellikleri Not Bu
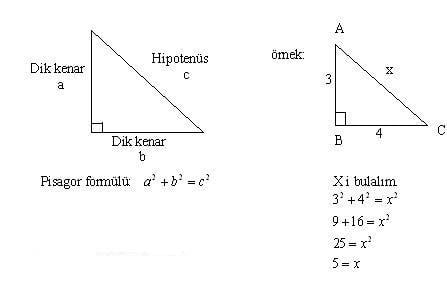



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Ozel Ucgenler Listesi
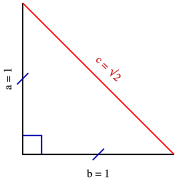



Dik Ucgen Vikipedi




Dik Ucgen Vikipedi




Matematik Panosundaki Pin




Dik Ucgen 15 45 45 90 Ucgeni Evde Egitim Ders Calisma Ipuclari Matematik




Nedir Dik Acili Ucgenin Kenar Ve Aci Ozellikleri



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube



Geodynamic Significance Of Granitoid Magmatism In The Southeast Anatolian Orogen Geochemical And Geochronogical Evidence From Goksun Afsin Kahramanmaras Turkey Region Springerlink



Ozel Ucgenler Konu Anlatimi




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube




Nature And Genesis Of Potassic High Basr Granitoids Associated With Syn Convergent Extension In Nw Turkey Sciencedirect




Acilarina Gore Ucgenler Ppt Indir
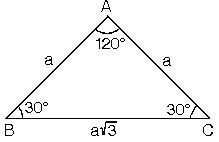



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



15 75 90 Ucgeni Turleri Ve Ozellikleri Ucgen Gen Tr


