
角度の求め方 算数の教え上手 学びの場 Com
Web 内角 (余弦定理) 半径 1 1 の球上にある球面三角形の内角 α α は、 によって与えられる。 ここで a,b,c a, b, c がそれぞれ球面三角形を成す弧の角度である (下の図を参考)。 この式を球面三角形に関する 余弦定理 という。 この関係式を用いると、 球面三角形の内角を中心角 (または弧の長さ)から求めることができる。 証明 原点 O O を中心とする半径 1 1 の球上にあるWeb 地盤周期の求め方比較してみました 国交省告示第1793号では、地盤周期に応じて地盤種別を判定する方法が書かれています。 このページでは、簡易計算で地盤周期を求める2つの方法を、計算例で比較していきます 『15年版建築物の構造関係技術基準
星形n角形 先端の角 一般式 求め方
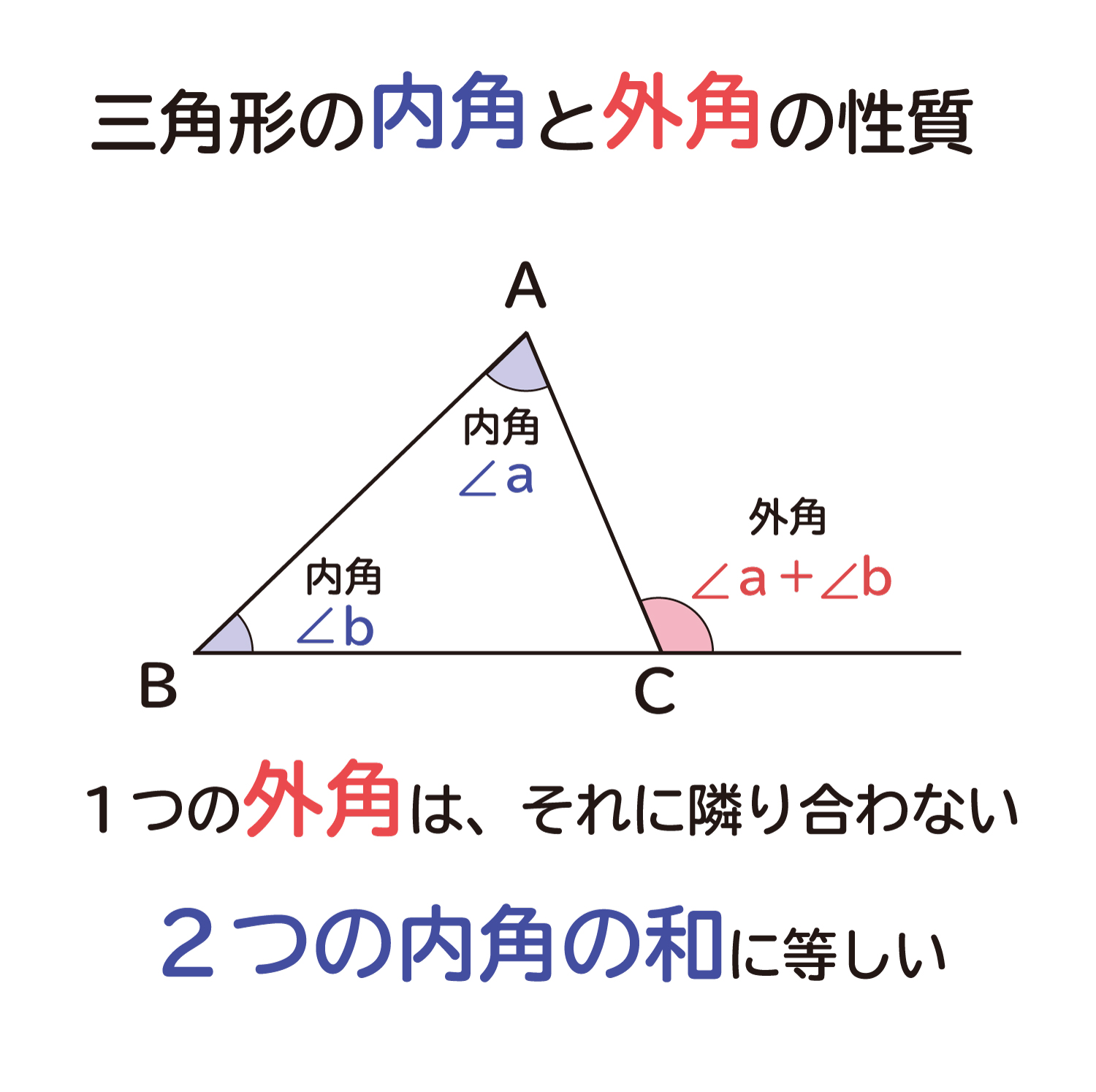
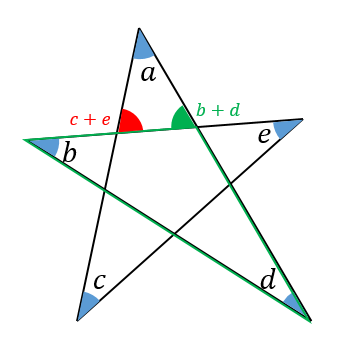
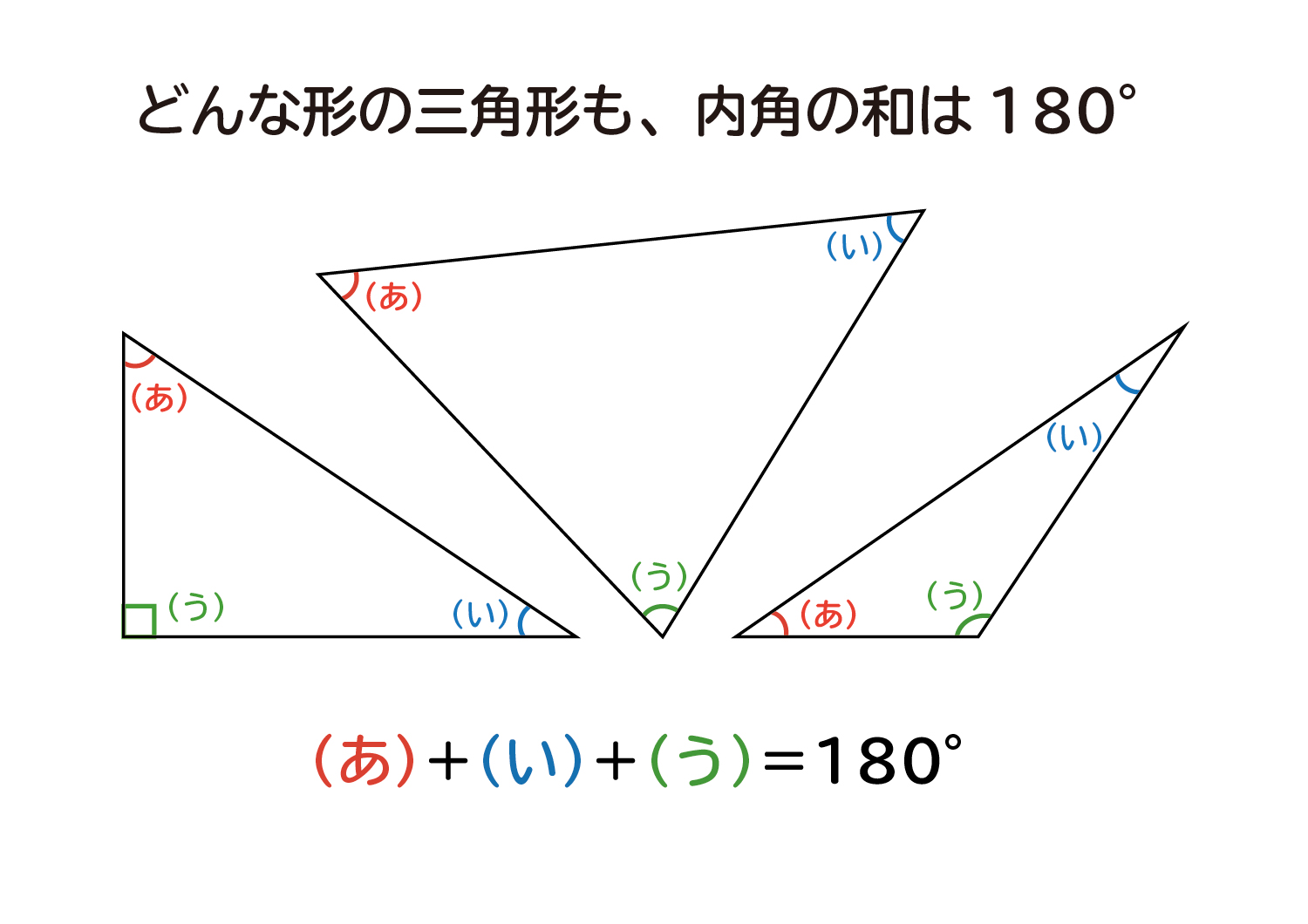
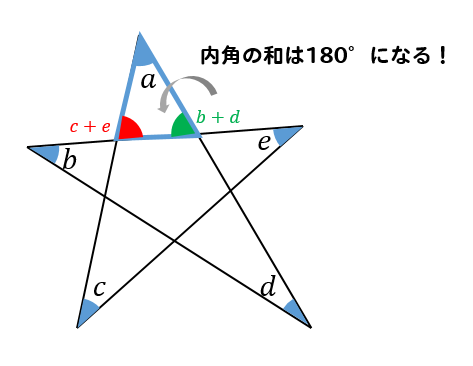
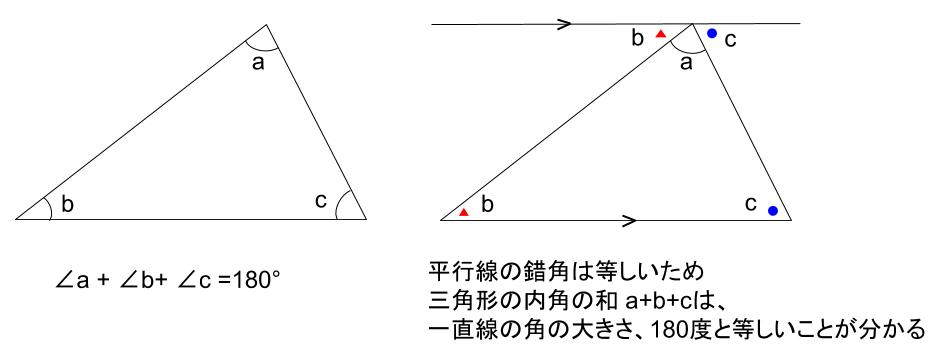
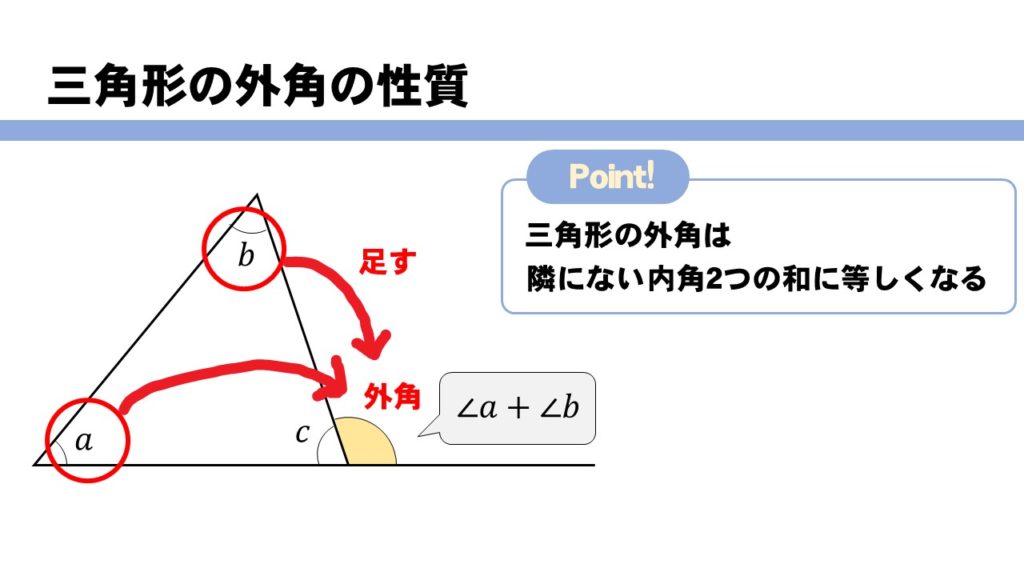
星形n角形 先端の角 一般式 求め方-Webこの記事では、三角関数の角度の求め方や変換公式(\(90^\circ − \theta\) など)についてわかりやすく解説していきます。 三角方程式・三角不等式の計算問題もていねいに説明していくので、この記事を通してぜひマスターしてくださいね!Web内角の和が180°になるということがわかります。 星形の図形では 三角形の外角の性質を利用していくと 全ての角を1つの三角形に集めることができるので 最終的には、和が180°! ということになります。 星形の角度問題に挑戦してみよう! それでは、星形の特徴がわかったところで 問題に挑戦してみましょう! の大きさを求めなさい。 解説&答えはこちら 星形の角度 まとめ

小学校5年 算数 四角形の内角の和 Youtube
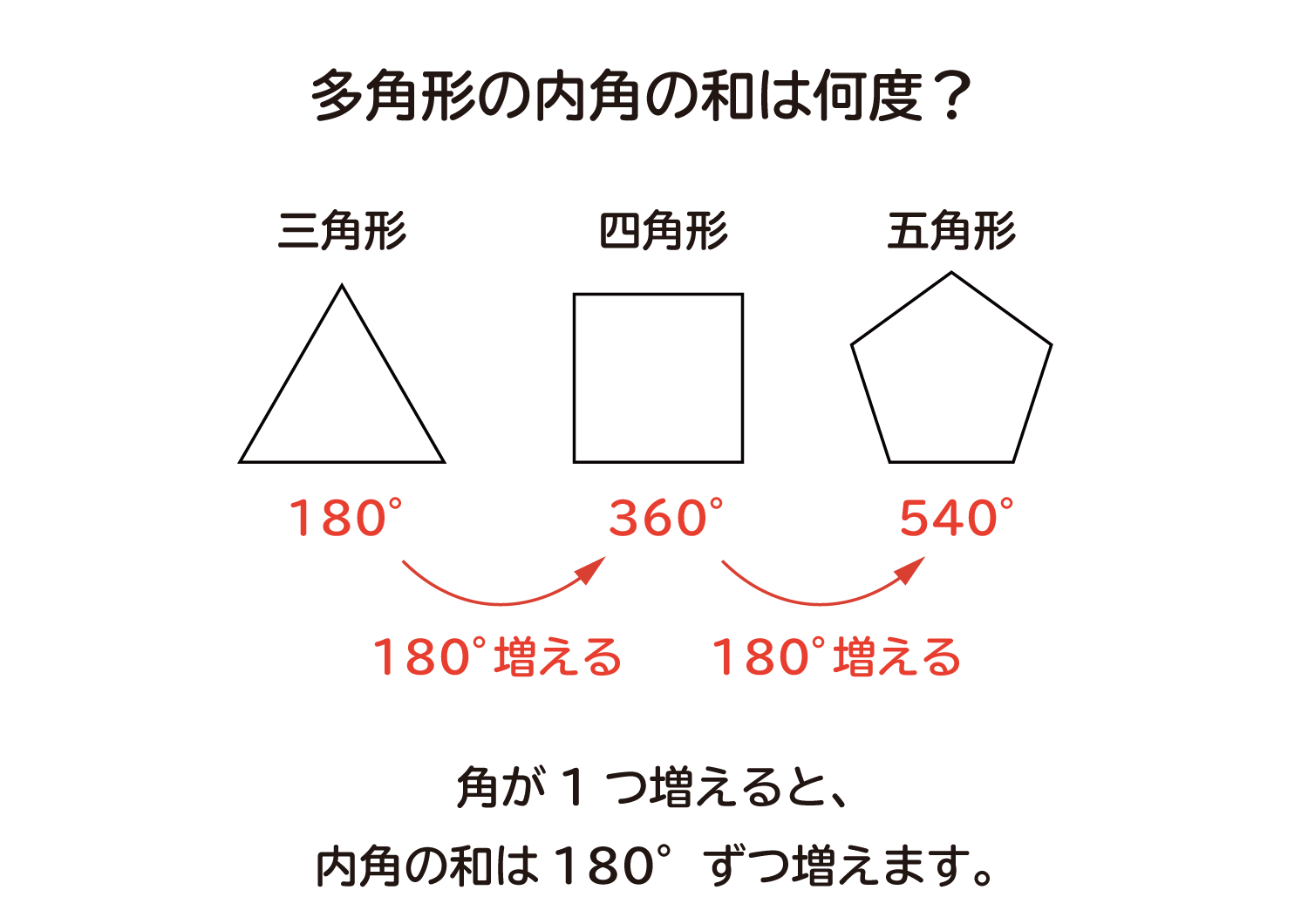
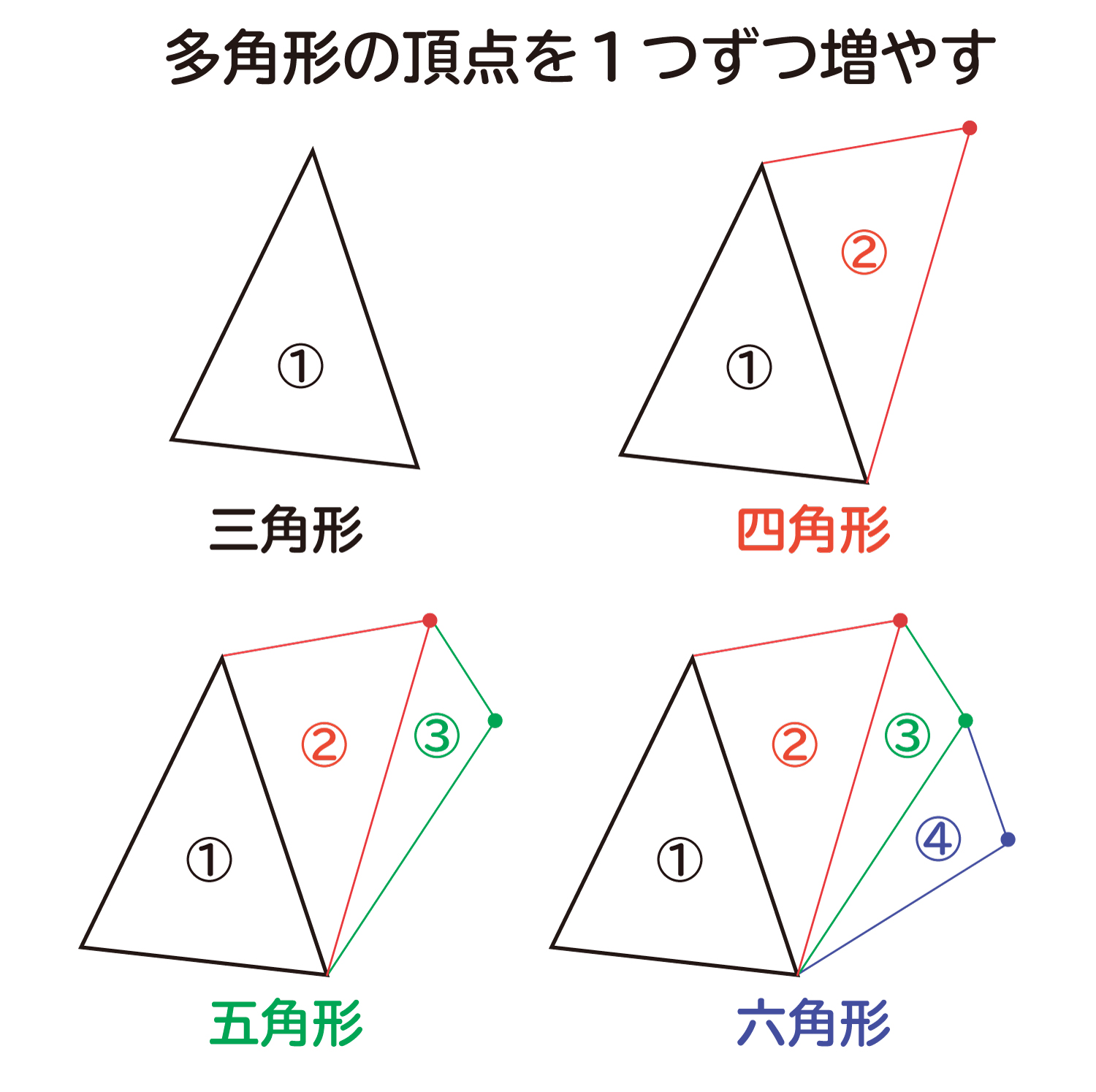
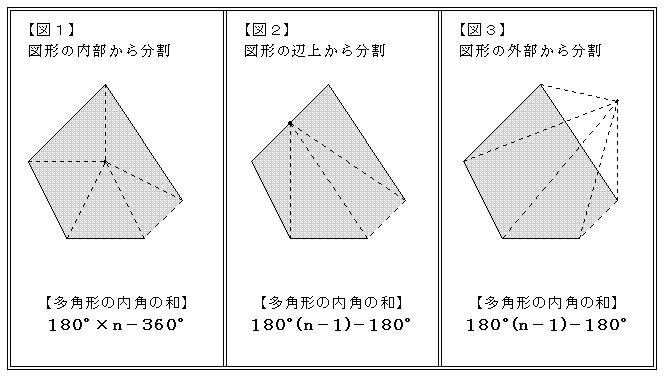
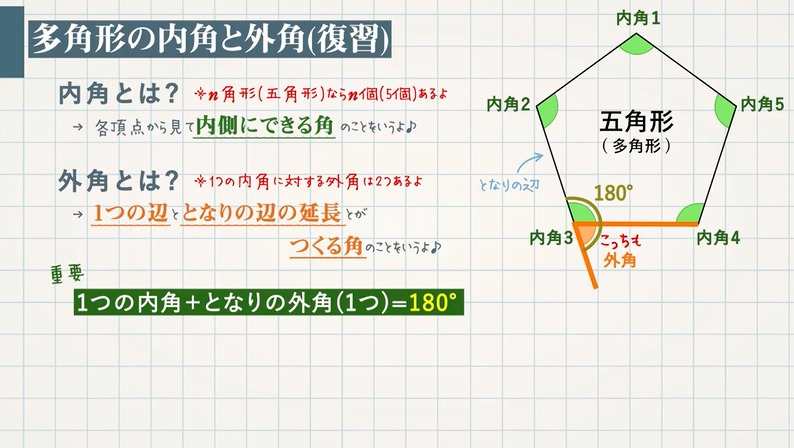
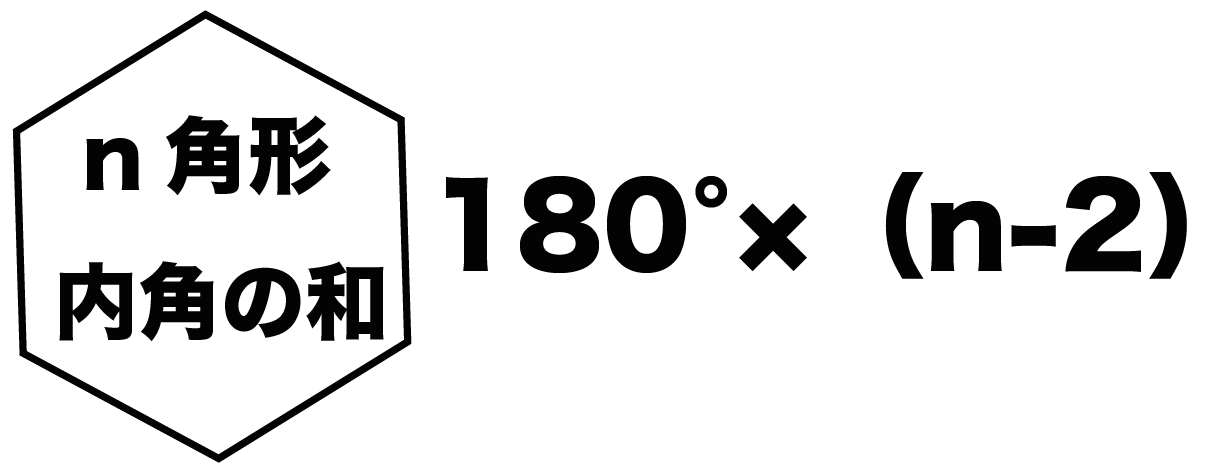
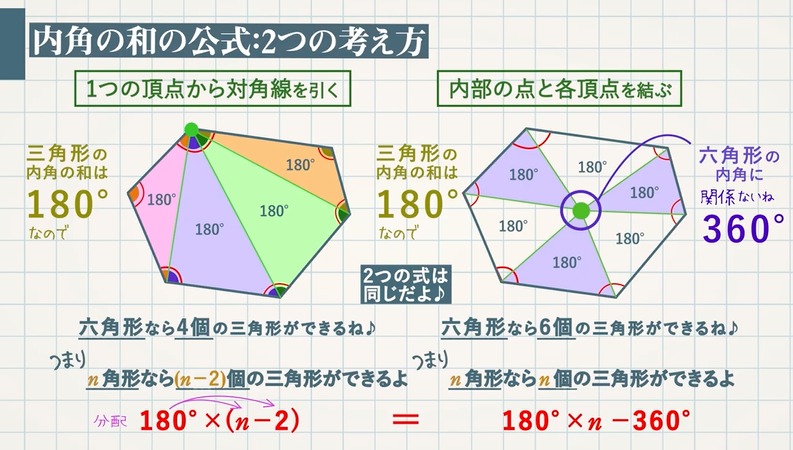
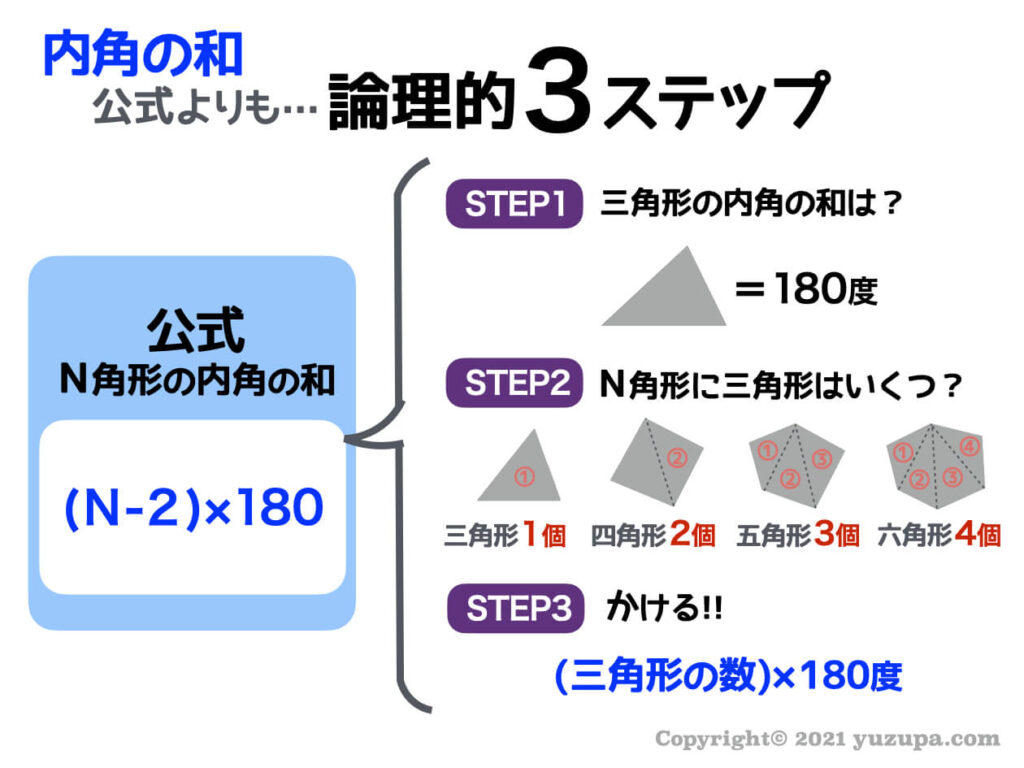
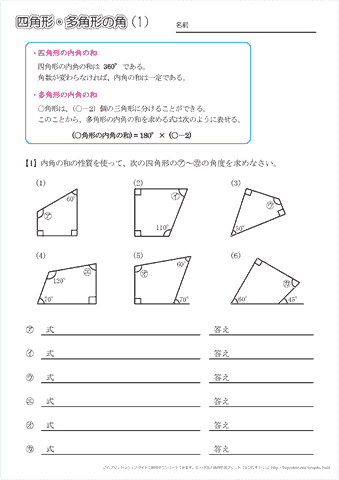
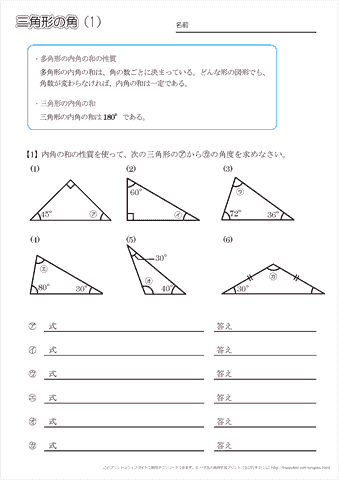
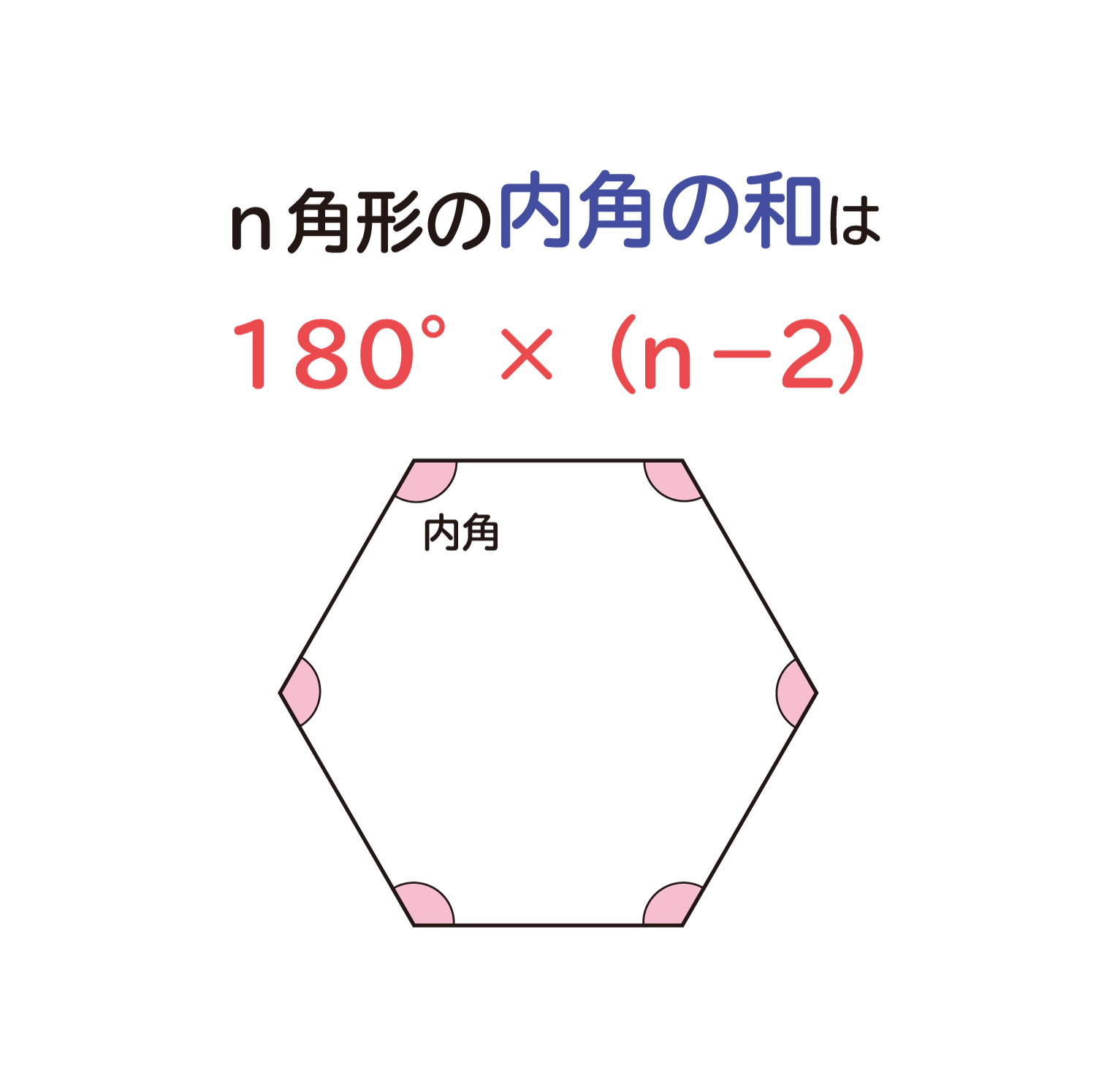
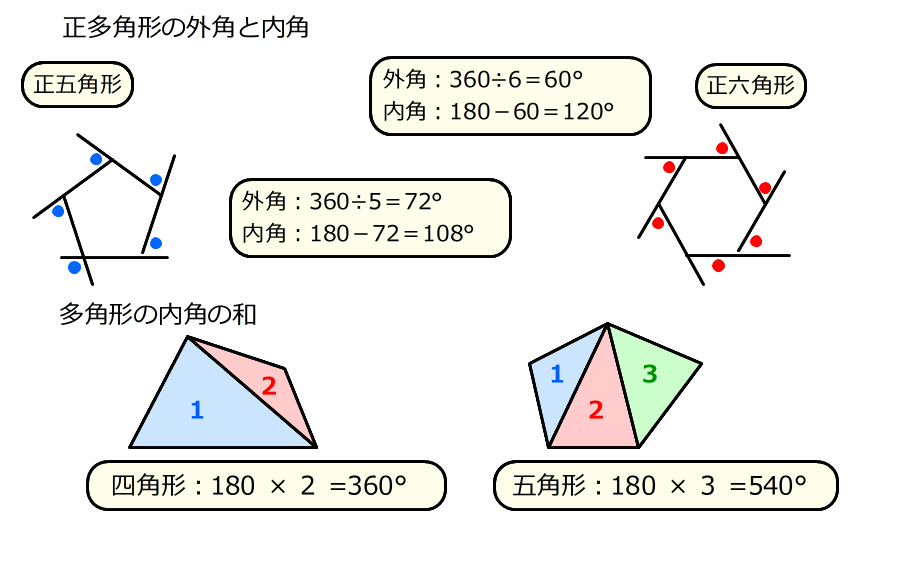
Web 正多角形の内角(外角)の求め方とは 正多角形とは、 「すべての辺の長さが等しく、すべての内角の大きさが等しい多角形」 を指します。 よって、多角形の内角の和の公式より、正多角形の一つ一つの内角は$$\frac{180°×(n2)}{n}$$と求めることができます。Web ⑤のやり方は、そのまま五角形の内角の和に応用できますね。 つまり、「多角形は、三角形に分けることで、内角の和を求めることができる」という点に気づかせてもおもしろいですね。 多角形の内角の和の授業についてはこちら (作成奮闘中)Web こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか
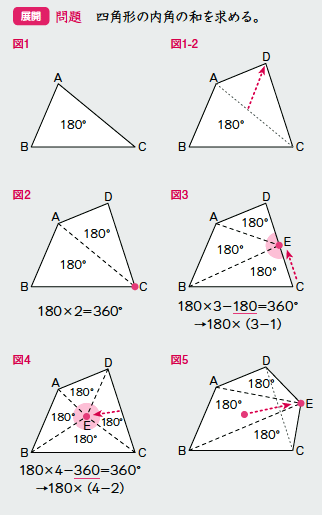
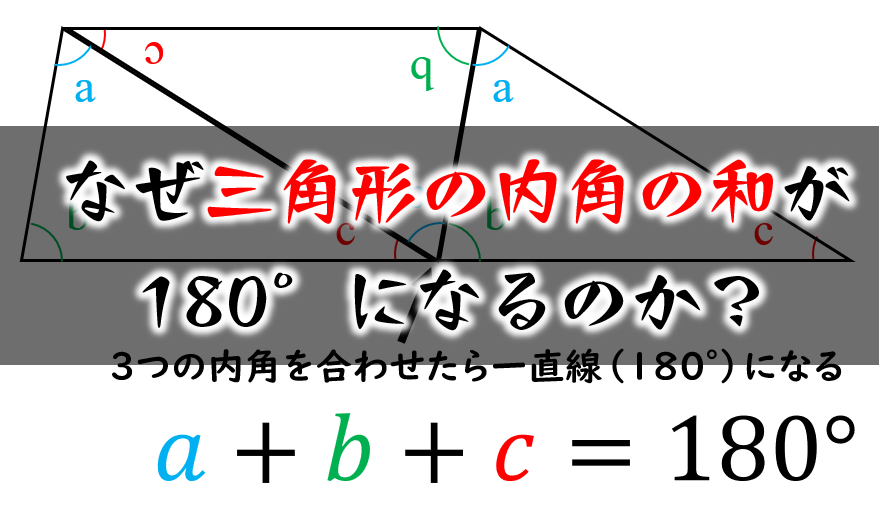
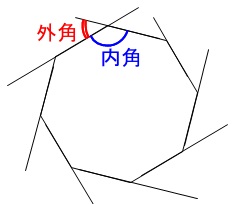
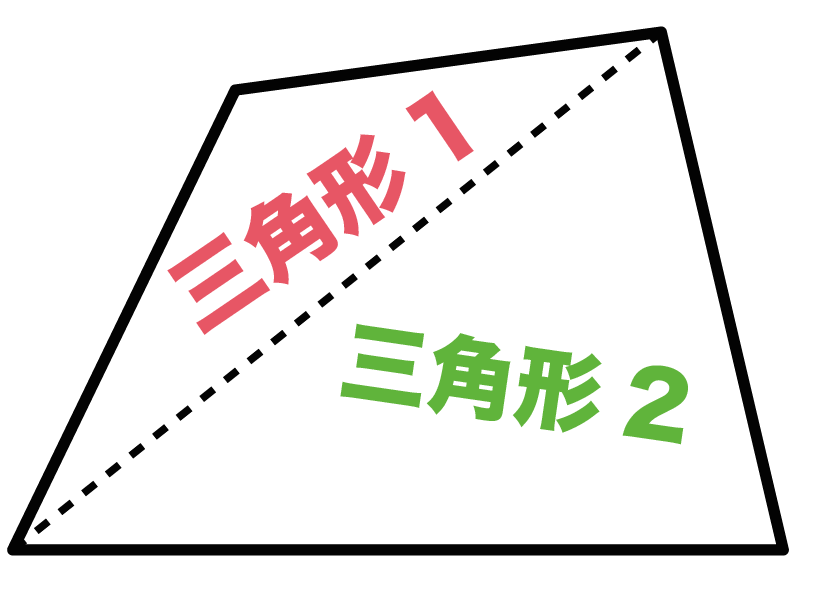
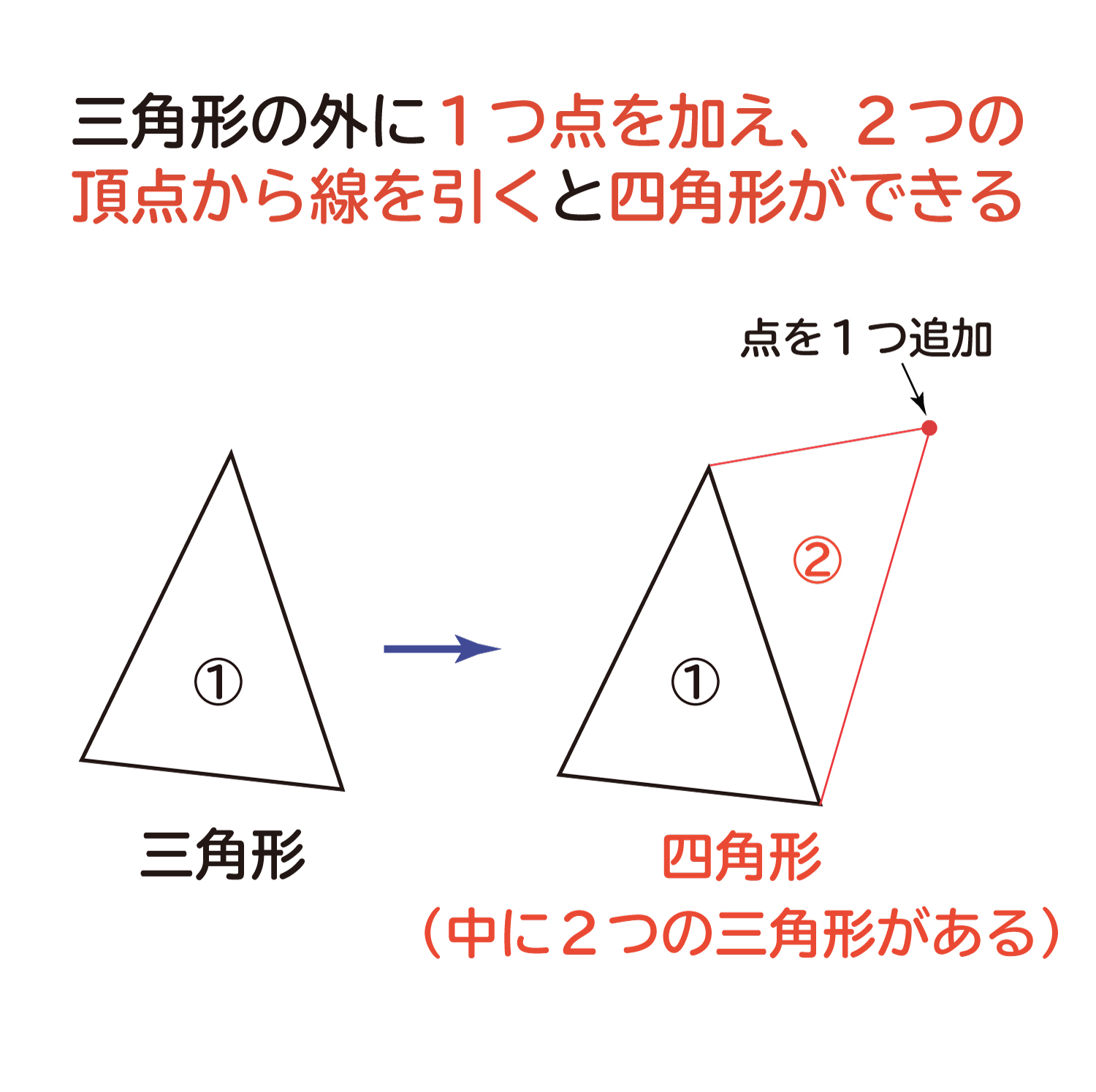
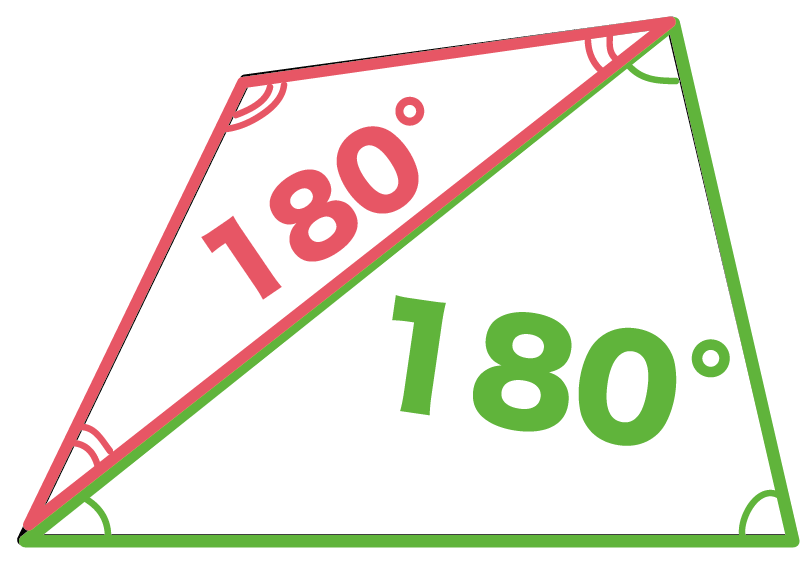
Web つまり、 正多角形の1つ分の内角は、内角の和を等分することで求めれます。 例 (正三角形) 内角の和180° ⇒ 1つ分の内角 (正六角形) 内角の和7° ⇒ 1つ分の内角 外角というものを利用すると、もっと簡単に求めることができます。 が、今回はWebこれだと面白くないので少し違う考え方をします。 下の図は台形ですが、 この四角形の内角の和を求めていきましょう。 この四角形の内角の和をどのように求めますか? ヒントは、三角形の内角の和を上手く使うことです。Web 四角形の内角の和の学習では、児童が初めて 演繹的な考え方 に出会います。 しかし、一般的な(教科書に載っている)展開は、児童の自然な思考の流れに反しています。 一般的な四角形の内角の和の授業は、 ①三角形の内角の和を帰納的に求める ②
星形n角形 先端の角 一般式 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 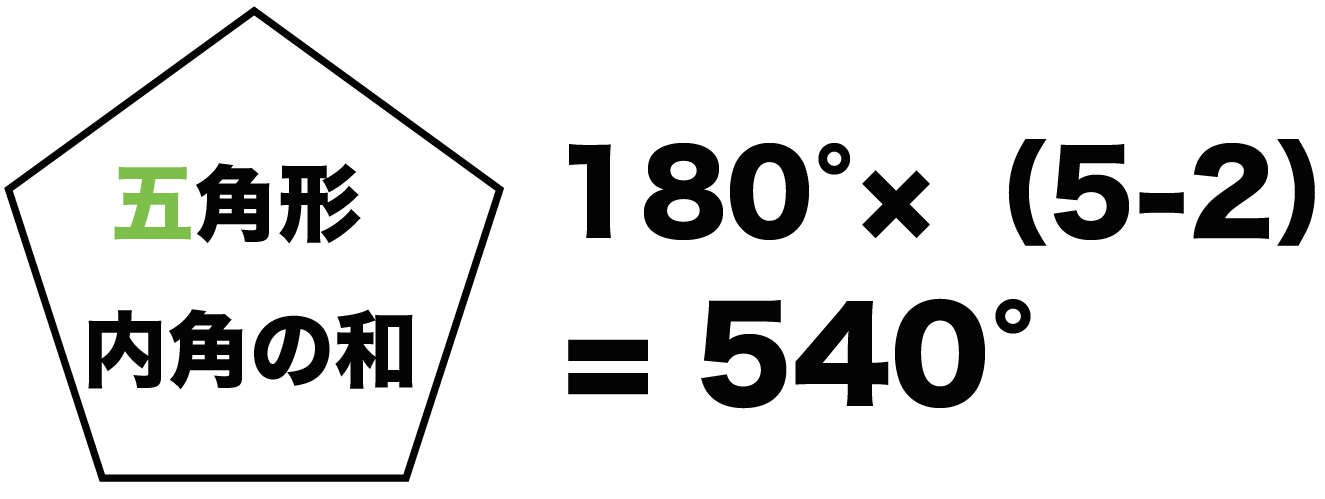 |  |
 |  |  |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「星形n角形 先端の角 一般式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
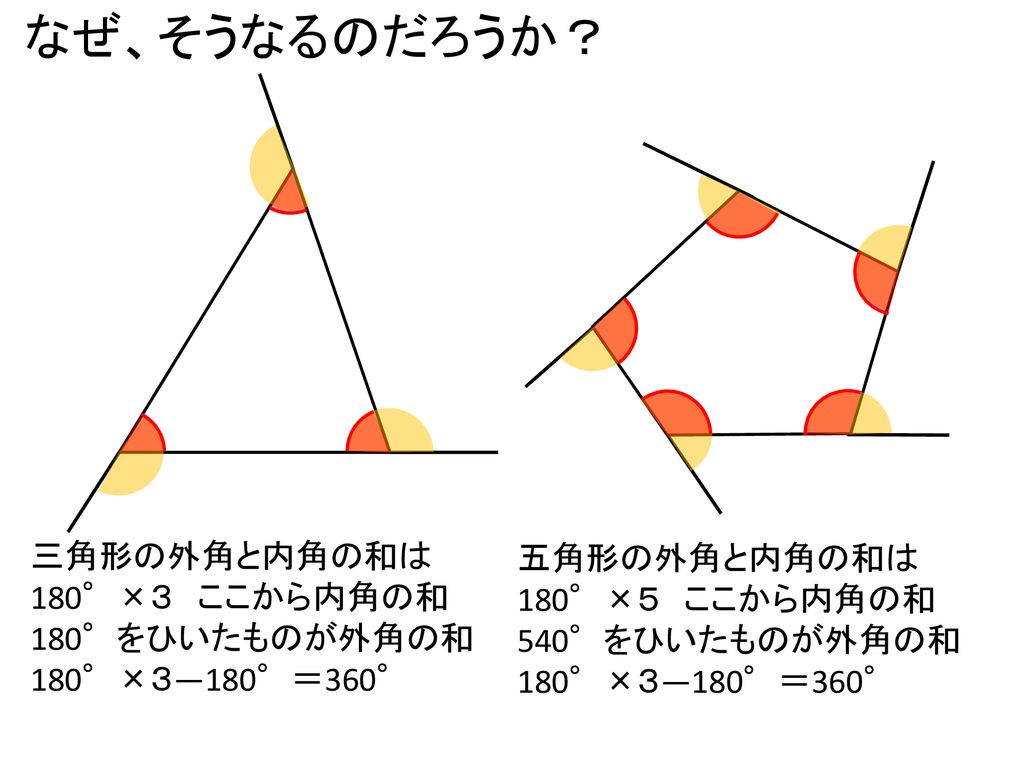 |
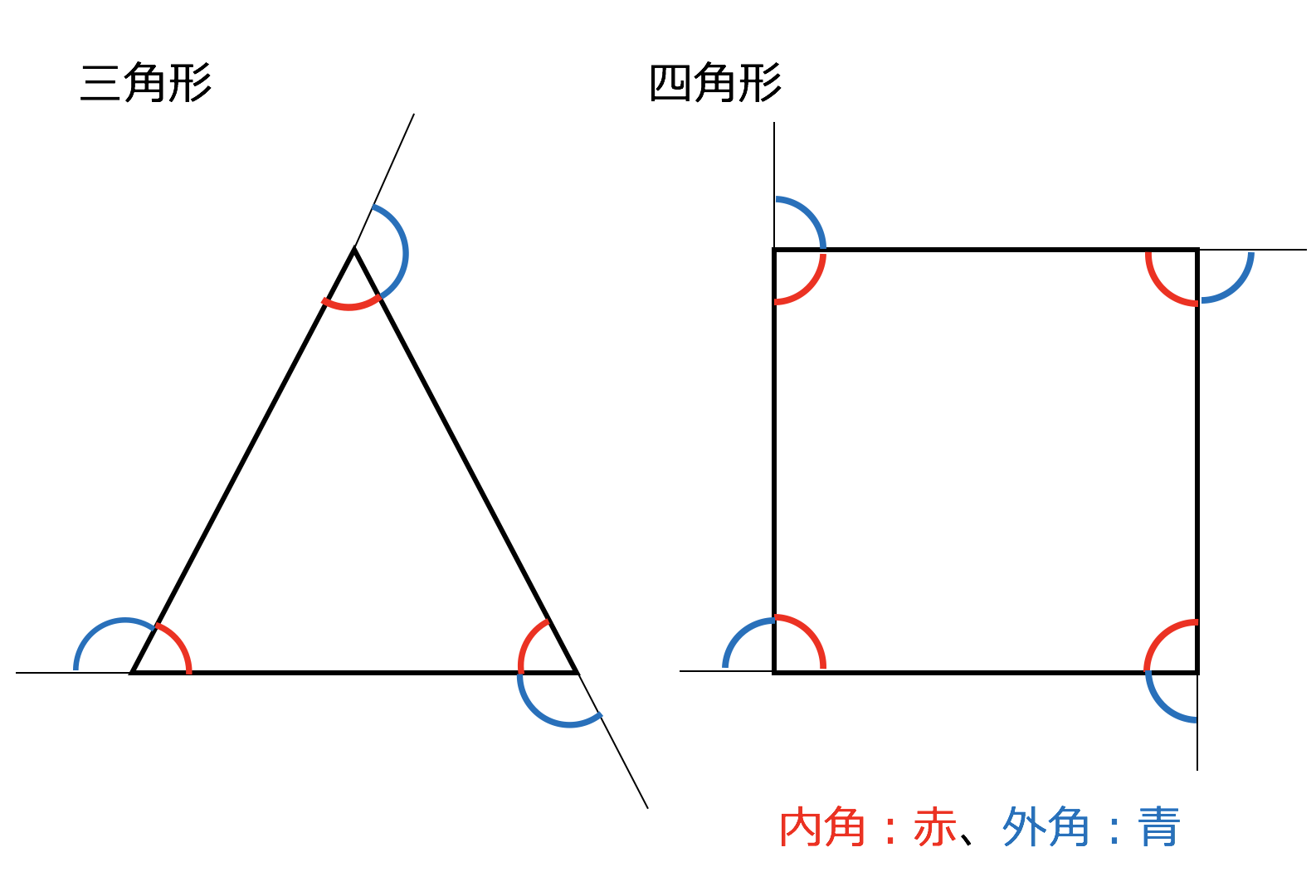
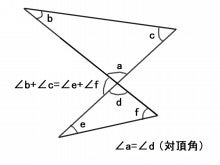
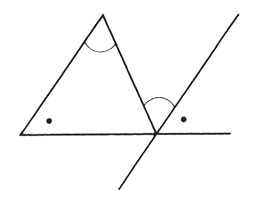
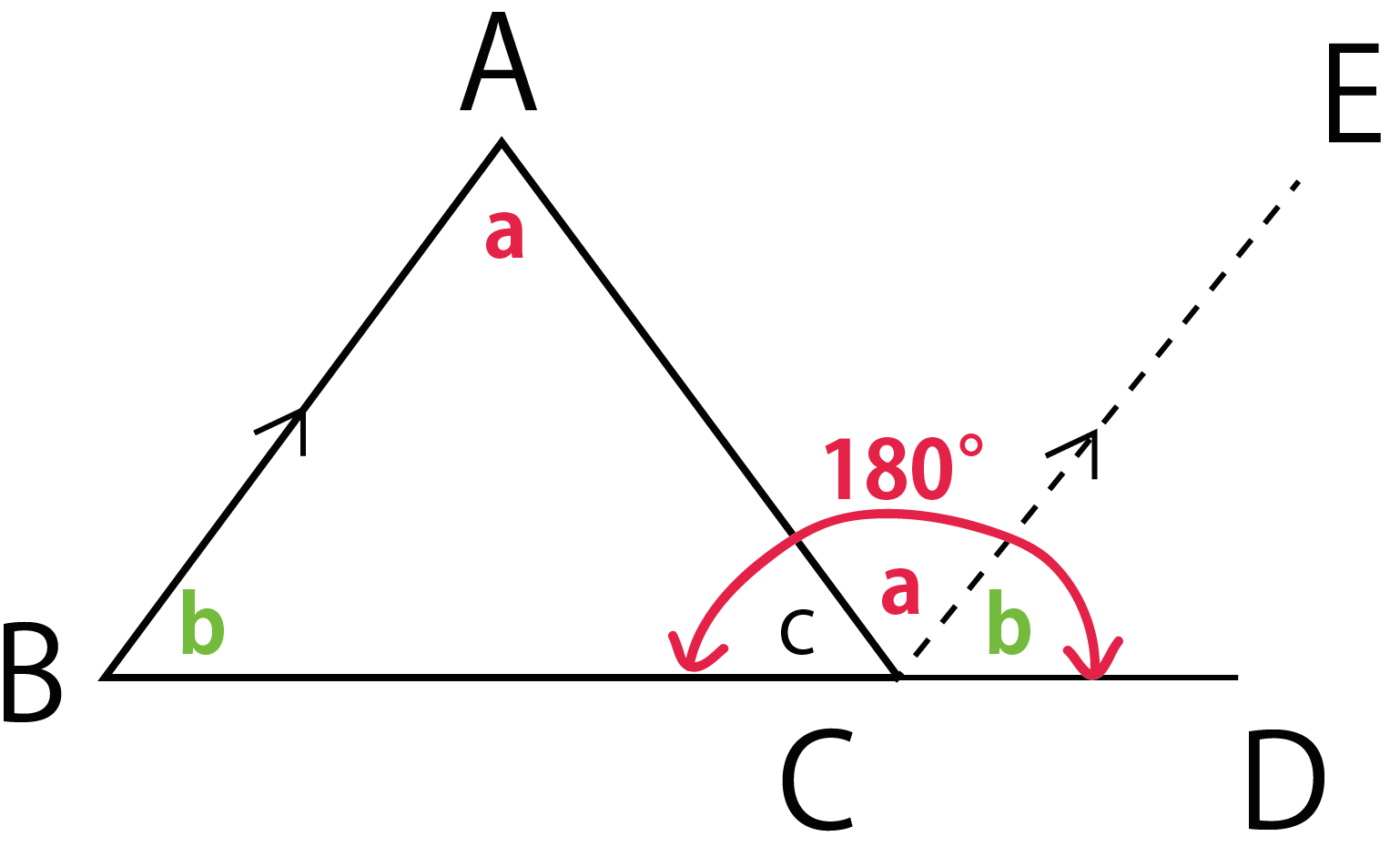
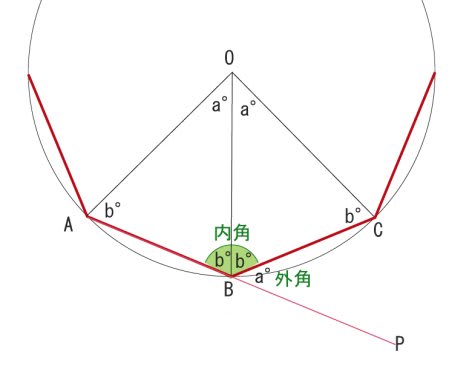
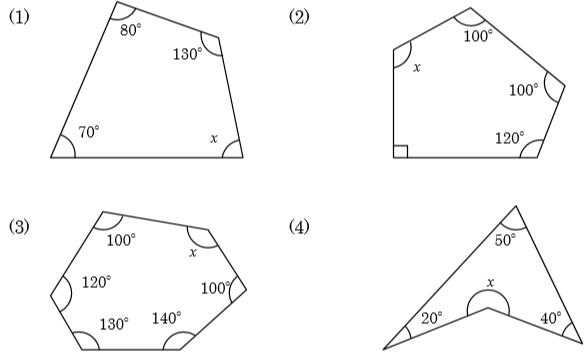
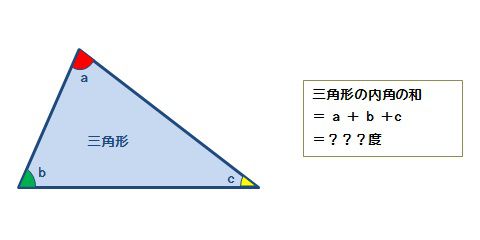
Webのはどんな条件のときか,調べてみましょう。 星形多角形の内角とは,多角形 の各辺の延長線でつくられた, 鋭角のみをいいます。 ∠a+∠b+∠c+∠d+∠e を 星形五角形の内角といいます。 星形多角形の内角 星形多角形Web 角B=180°-(30°+45°) =180°-75° =105° と計算できます。 この角Aように、あらかじめわかる角度を図に記入して、三角形の内角と外角の関係(三角の旗)を利用すると簡単に正解が得られる問題はたくさんあります。 答え 角A=1°、角B=105°
Incoming Term: 内角の求め方, 内角の求め方 公式, ベクトル 内積 なす角 求め方, 星形n角形 先端の角 一般式 求め方, 直角三角形 内接円 半径 求め方, 多角形の内角の和 小学 算数 教え方, 中2 数学 角度の求め方 応用, 円に内接する 正八 角形 面積, 直角三角形 角度 求め方 中学生,



